Question

Постройте график функции y=6-4x-2x^2 Найдите: а) область значений функции; б) при каких значениях аргумента функция возрастает.

Answer 1

а).  

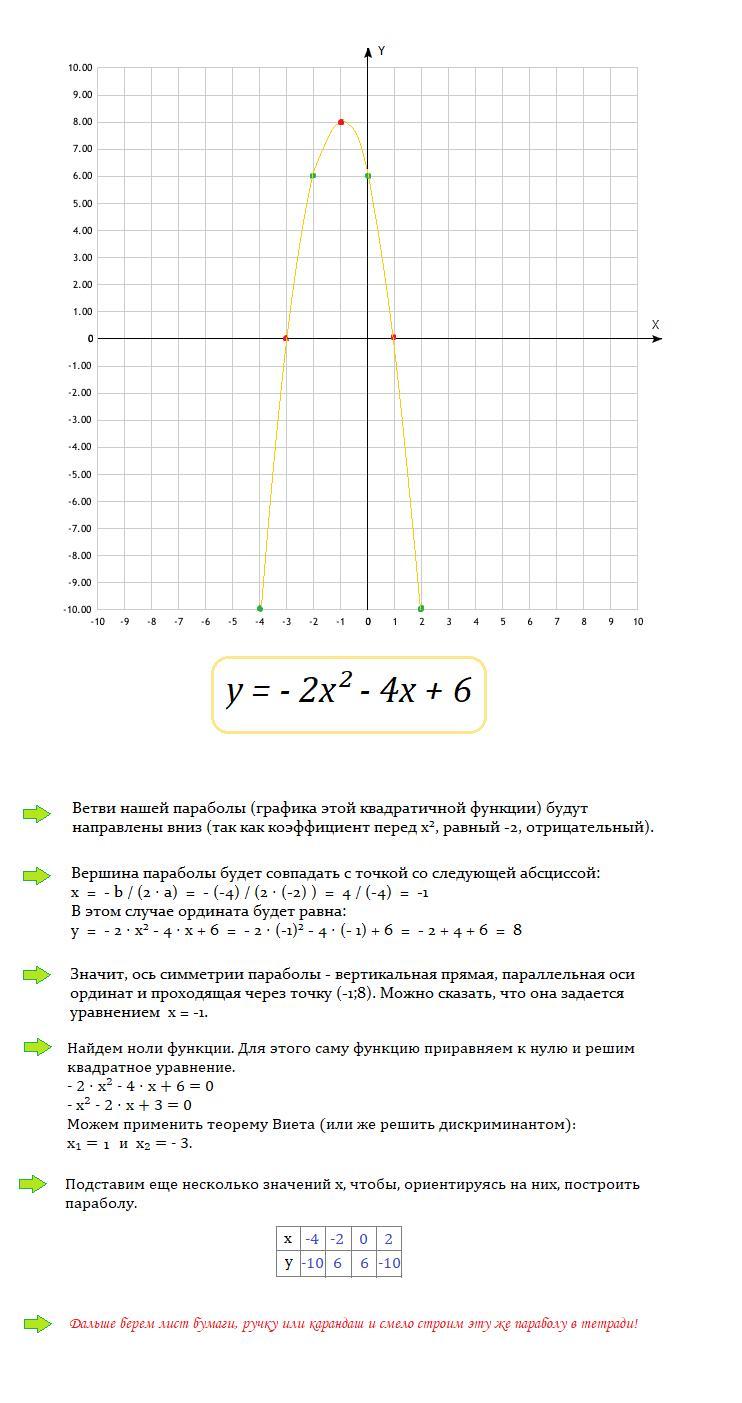
Сначала построим график функции $y = -2x^2 - 4x + 6$ (в первом файле - сам график, а во втором файле - этот же график, но с этапами построения).

Область значений функции - это все возможные значения, которые может принимать функция (то есть, те значения $y$, при которых функция существует).

Отсюда следует, что область значений данной функции равна (это можно определить, посмотрев на график):

$\boxed {E(y) = (- \infty ; 8 \; ]}$

б).

Если мы посмотрим на график,то окажется, что:

• при $x \in (-\infty ;-1 \; ]$ функция растет;
• при $x \in [ \; -1 ; + \infty )$ функция убывает.

(В точке  $x = -1$  достигается точка максимума функции)

И ответ на задачу: функция возрастает на промежутке

$\boxed {x \in ( - \infty ; -1 \; ]}$