1) Отрезок перресекает плоскость, концы отрезка удалены от плоскости на расстоянии 8 см и 2 см. Найти расстояние середины отрезка.
2) Из точки, отстоящей от плоскости на расстоянии 3 см, проведены 2 наклонные
образующие с плоскостью углы 45 и 30 градусов, а между собой прямой угол. Определить расстояние между концами наклонных.
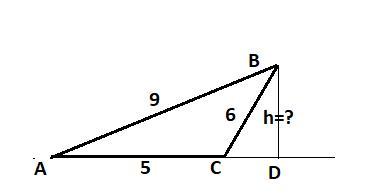
3) Дан треугольник ABC со сторонам AB= 9 см, BC=6 см, AC=5 см. Через сторону АС проходит плоскость М, составляющая с плоскостью треугольника угол 45 градусов. Найти расстояние от вершины B до плоскости М.
Ответы
Ответ:
Пошаговое объяснение:
1. Найти середину отрезка.
Рисунок к задаче в приложении.
Три варианта формул:
1) С = (А+В)/2 = (8+2)/5 = 5 - ответ.
2) С = В + (А-В)/2 = 2 + (8-2)/2 = 5 - ответ
3) С = А - (А-В)/2 = 8 - (8-2)2 = = 5 - ответ
2. Наклонные
Рисунок к задаче в приложении.
Применяем тригонометрические формулы.
AD/BD = tgβ = tg 45° = 1
BD = AD = 3 - отрезок
AD/CD = tg30° = √3/2
AD = 3√3/2 - отрезок
ВС = 3(√3/2 -1) = 3/2*(√3 - 2) - длина отрезка - ответ.
3. расстояние ВМ - равно высоте h(B) треугольника АВС.
Формула для высоты h(B):
p = (a+b+c)/2 = 10
(p-a) = 4 и (p-b) = 5 и (p-c) = 1
Под корнем = 200
BD = h(b) = 2/5*√200 - высота в треугольнике.
Наклоняем треугольник на 45° и высота становится гипотенузой.
BM = BD*cos45° = 2/5√200*√2/2 = √100/5 = 10/5 = 2 высота - ответ