Предмет: Алгебра,
автор: asya20181
СРОЧНО
СРОЧО
как найти MAX функции
y=-79-18x-x^2 все это в корне
Ответы
Автор ответа:
3
Решение:
- Заметим, что максимальное значение функции
достигается при том же значении
, что и максимальное значение функции
(при условии, что значение последней при данном
неотрицательно).
Найти максимальное значение функции несложно: раз функция квадратичная и коэффициент при
(
) отрицательный, то максимальное значение достигается в вершине ее параболы, координаты
которой поддаются вычислению:
Значит:
,
.
Задача решена!
Ответ: √2 .
Приложения:
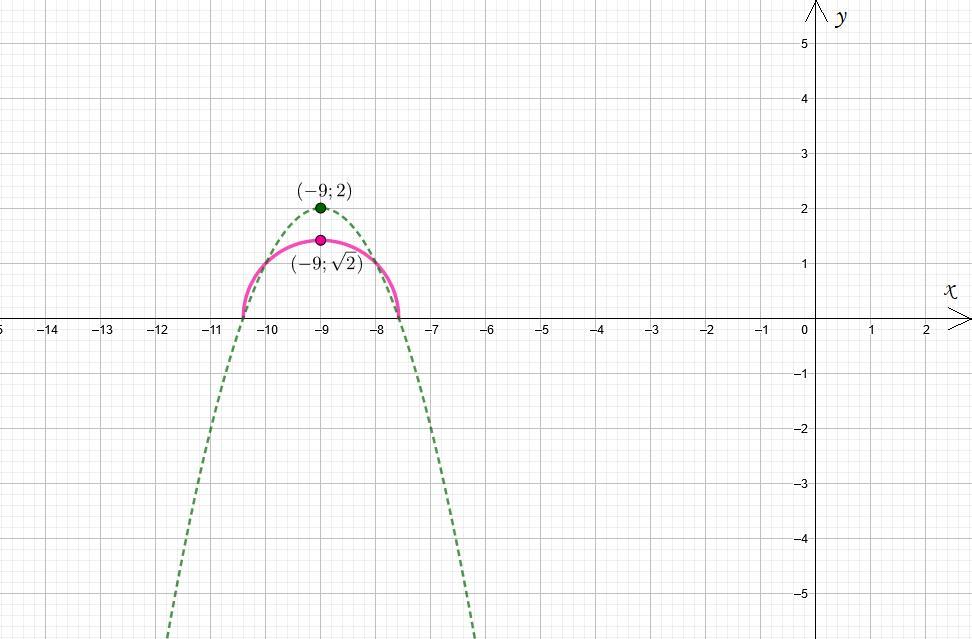
Автор ответа:
4
Ответ:
max{y}=y(-9)=
Объяснение:
Рассматривается функция
Определим максимальное значение функции следующим образом:
Равенство в неравенстве достигается когда x+9=0, то есть при x= -9. Отсюда, максимальное значение функции равен .
Похожие вопросы
Предмет: Математика,
автор: simpleplay129
Предмет: Алгебра,
автор: lerapasat8
Предмет: Русский язык,
автор: vovashkaruba
Предмет: Математика,
автор: светлана2351