Предмет: Математика,
автор: LSM54
ПОМОГИТЕ!! Тригонометрия! 100 БАЛЛОВ!!
Приложения:
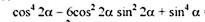
NNNLLL54:
там, наверное, описка, не sin^4(a), а sin^4(2a)
Ответы
Автор ответа:
2
Вообще-то, сразу можно было написать по формуле косинуса двойного угла:
Не стираю только для того, чтобы посмотрели как можно упрощать сумму и разность sin и cos.
Похожие вопросы
Предмет: Окружающий мир,
автор: av2654257
Предмет: Математика,
автор: kkv68032
Предмет: Другие предметы,
автор: snezannamesankina
Предмет: Математика,
автор: Казна11
Предмет: Физика,
автор: Zhenehka11