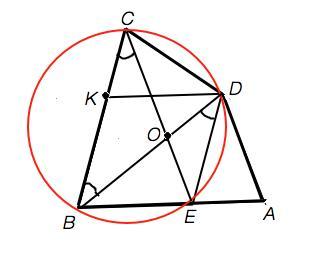
В выпуклом четырехугольникe ABCD углы при вершинах A, B , C равны 80 градусов . На стороне AB отмечена точка Е . Известно, что AD=CD=BE . Найдите угол BCE. Обоснуйте решение
Ответы
Сумма углов четырехугольника 360°. Поэтому ∠СDА=360°-3•80°=120°. Проведем DК||ВЕ. ∠DКС =∠CBE=80° как соответственные при пересечении параллельных прямых секущей, поэтому ∆ СDК равнобедренный, ∠CKD=∠KCD=80° ⇒ ∠СDК=180°-2•80°=20° и КD=СD, поэтому КD=ВЕ,. В четырехугольнике ВКDЕ противоположные стороны КD и ВЕ равны и параллельны ⇒ ВКDЕ - параллелограмм. ∠КDЕ=КВЕ=80°, а ∠ЕDА=120°- ∠СDK-∠КDE ∠ЕDА=120°-20°-80°=20°. . Из суммы углов треугольника ∠АЕD=180°-20°-80°=80°⇒ DE=DA. Все стороны параллелограмма ВКDЕ равны, следовательно он - ромб. Диагонали ромба - биссектрисы его углов. ∠КВD =∠ВDЕ=80°:2=40°.
Т.к. ВС||DE, четырехугольник BCDE - трапеция. Вокруг равнобедренной трапеции можно описать окружность. Вписанные углы ВСЕ и ВDЕ опираются на одну дугу ВЕ ⇒ ∠ВСЕ=∠ВDЕ=40°
Или
Диагонали равнобедренной трапеции равны и при пересечении образуют с основаниями равнобедренные треугольники. Поэтому ∆ ВСО - равнобедренный , угол ВСЕ=СВЕ и равны накрестлежащему ВDЕ =40°