Предмет: Алгебра,
автор: dusha
решите уравнение
sin (5/3П*cosПx) = 1/2
Приложения:
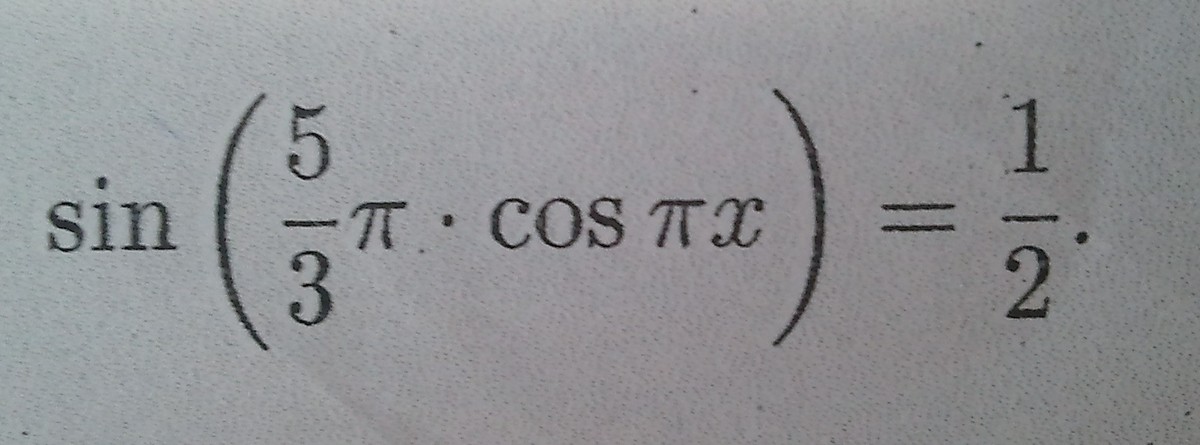
Ответы
Автор ответа:
0
sin (5/3П*cosПx) = 1/2
5/3Пi*cos (pix) =(-1)^k * pi/6+pi*k, где k - целое
сos (pix) =(-1)^k /10+3/5 *k, где k - целое
так как область значений косинуса от -1 включительно до 1 включительно, то последнее уравнение равносильно следующим уравнениям
k=1: сos (pix) =0.5
k=0: сos (pix) =0.1
k=-1: сos (pix) =-0.7
c первого
pi x =(+/-) pi/3+2*pi*l, где l - целое
x=(+/-)1/3+2l, где l - целое
со второго
pi x=(+/-)arccos 0.1+2*pi*n, где n - целое
x=(+/-)1/pi *arccos 0.1+2*n, где n - целое
с третьего
pi x=(+/-)arccos (-0.7)+2*pi*m, где m-целое
x=(+/-)1/pi *arccos (-0.7)+2*m,где m - целое
ответ: (+/-)1/3+2l, где l - целое
(+/-)1/pi *arccos 0.1+2*n, где n - целое
(+/-)1/pi *arccos (-0.7)+2*m,где m - целое
Похожие вопросы
Предмет: Кыргыз тили,
автор: eguaros97
Предмет: Информатика,
автор: Аноним
Предмет: Русский язык,
автор: zvezdocka42
Предмет: Математика,
автор: Серёга154
Предмет: Биология,
автор: Alyona3108