Question

Нужно решить показательное уравнение.
5^x + 12^x = 13^x

Answer 1

$5^x+12^x=13^x \\ \frac{5^x}{12^x}+1=\frac{13^x}{12^x} \\ g(x)=\frac{5^x}{12^x}+1 \ ; \ f(x)=\frac{13^x}{12^x}$

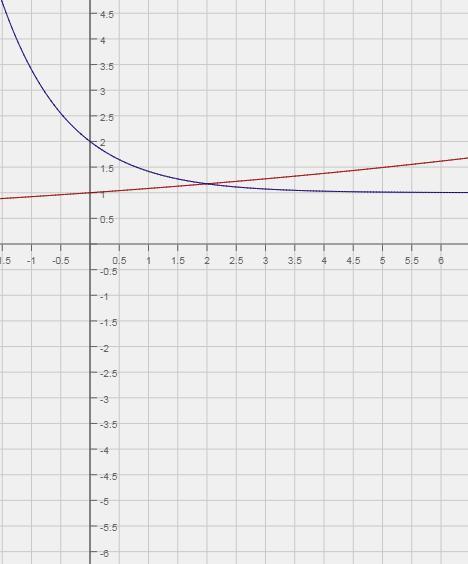
g(x) - монотонно убывающая функция; f(x) - монотонно возрастающая функция

При x=2  g(x)=f(x)

При x<2  g(x)>f(x)

При x>2  g(x)>f(x)

числа 5, 12, 13 являются Пифагоровой тройкой:

$5^2+12^2=13^2 \\ 25+144=169 \\ 169 = 169$

Ответ: x = 2