Предмет: Алгебра,
автор: kirill4272
Помогите срочно надо дам корону!!!к
Приложения:

Ответы
Автор ответа:
1
Приложения:
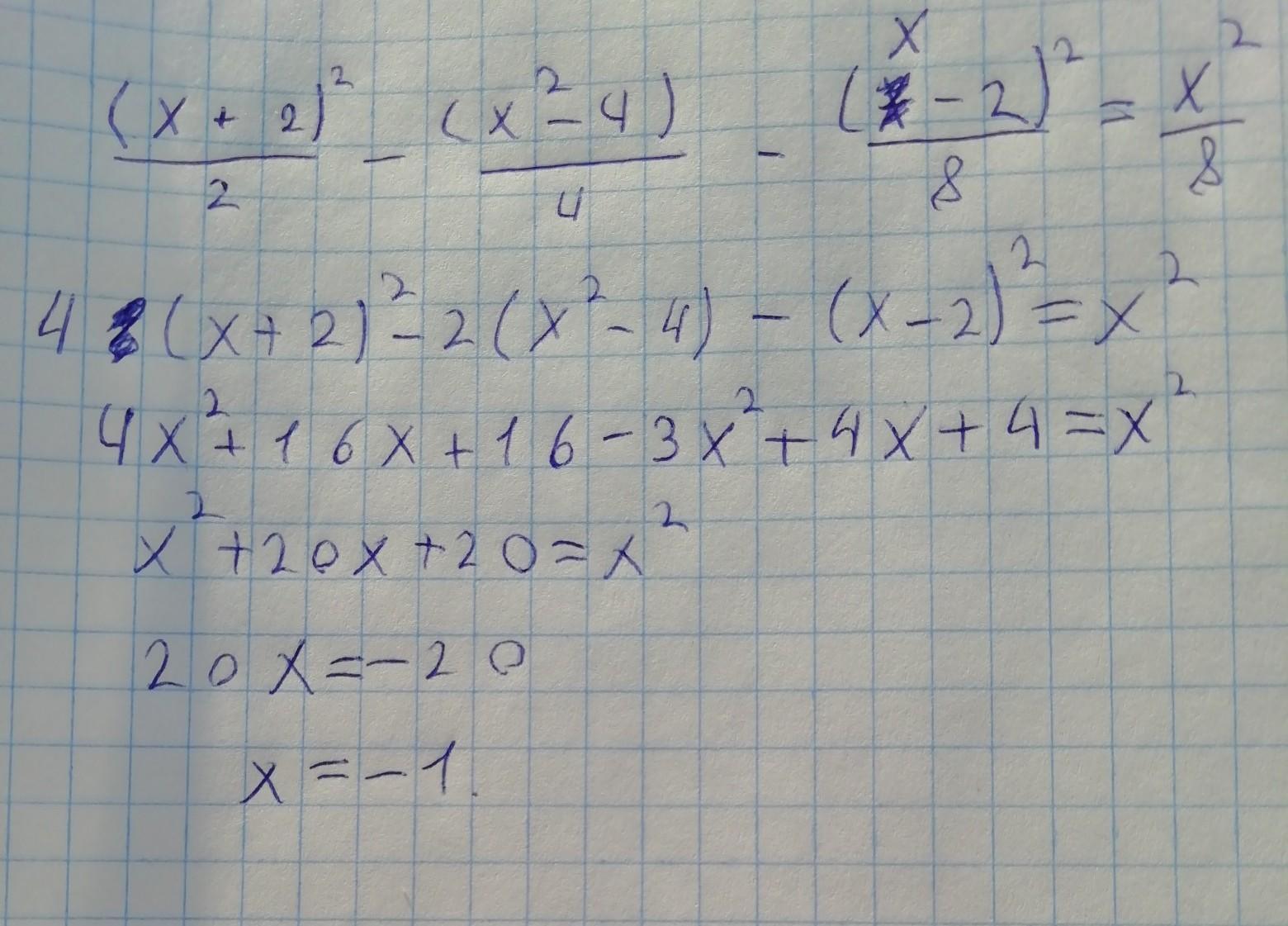
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: vlada91vl
Предмет: Английский язык,
автор: ks8022407
Предмет: Литература,
автор: 012345678910111
Предмет: Литература,
автор: Stefanolga