Question

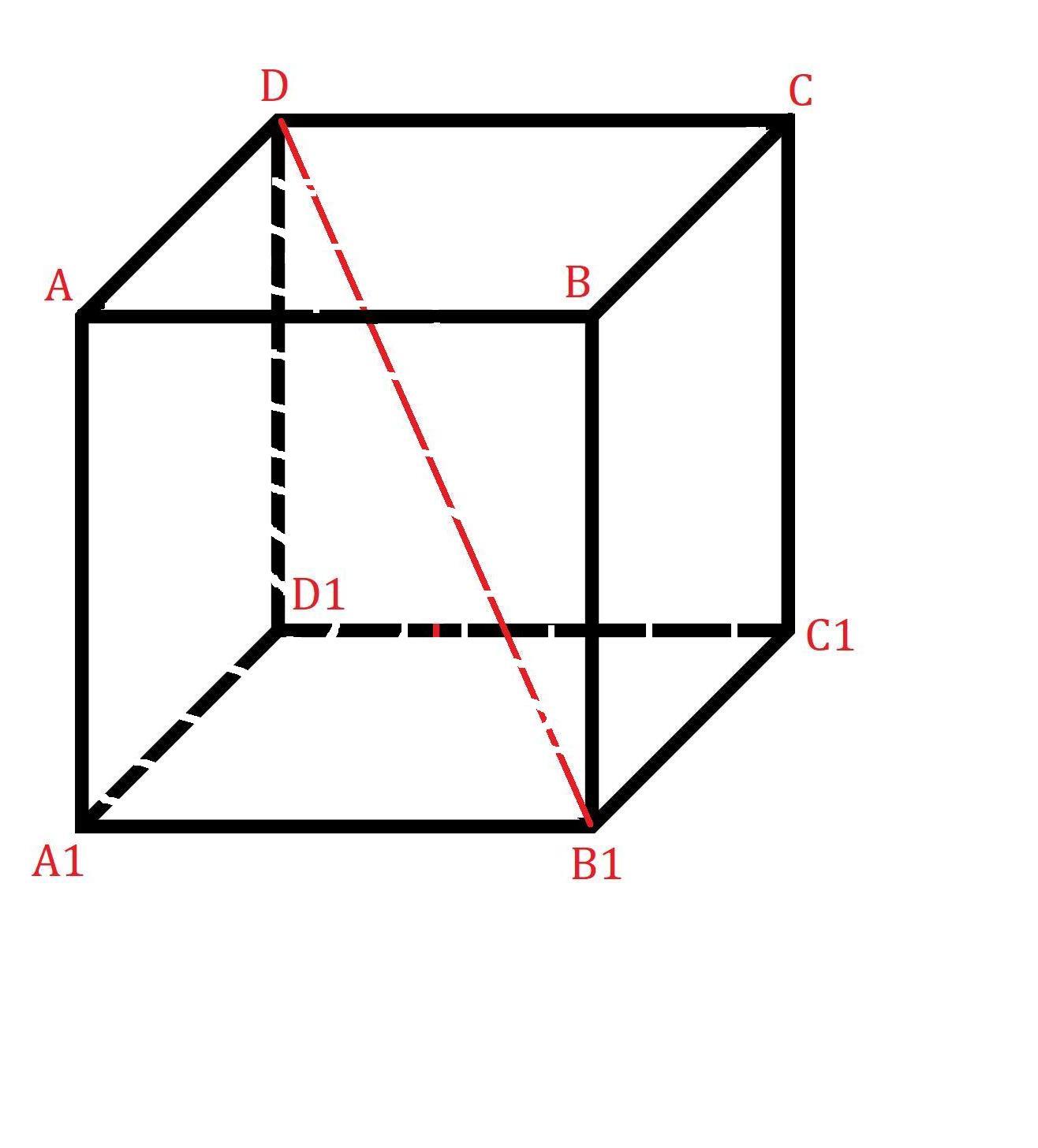
Дан прямоугольный параллелепипед АВСDА1В1С1D1. Найдите диагональ параллелепипеда, если его измерения таковы: 4 см, 2 см, 4 см. Постройте общий перпендикуляр скрещивающихся прямых:

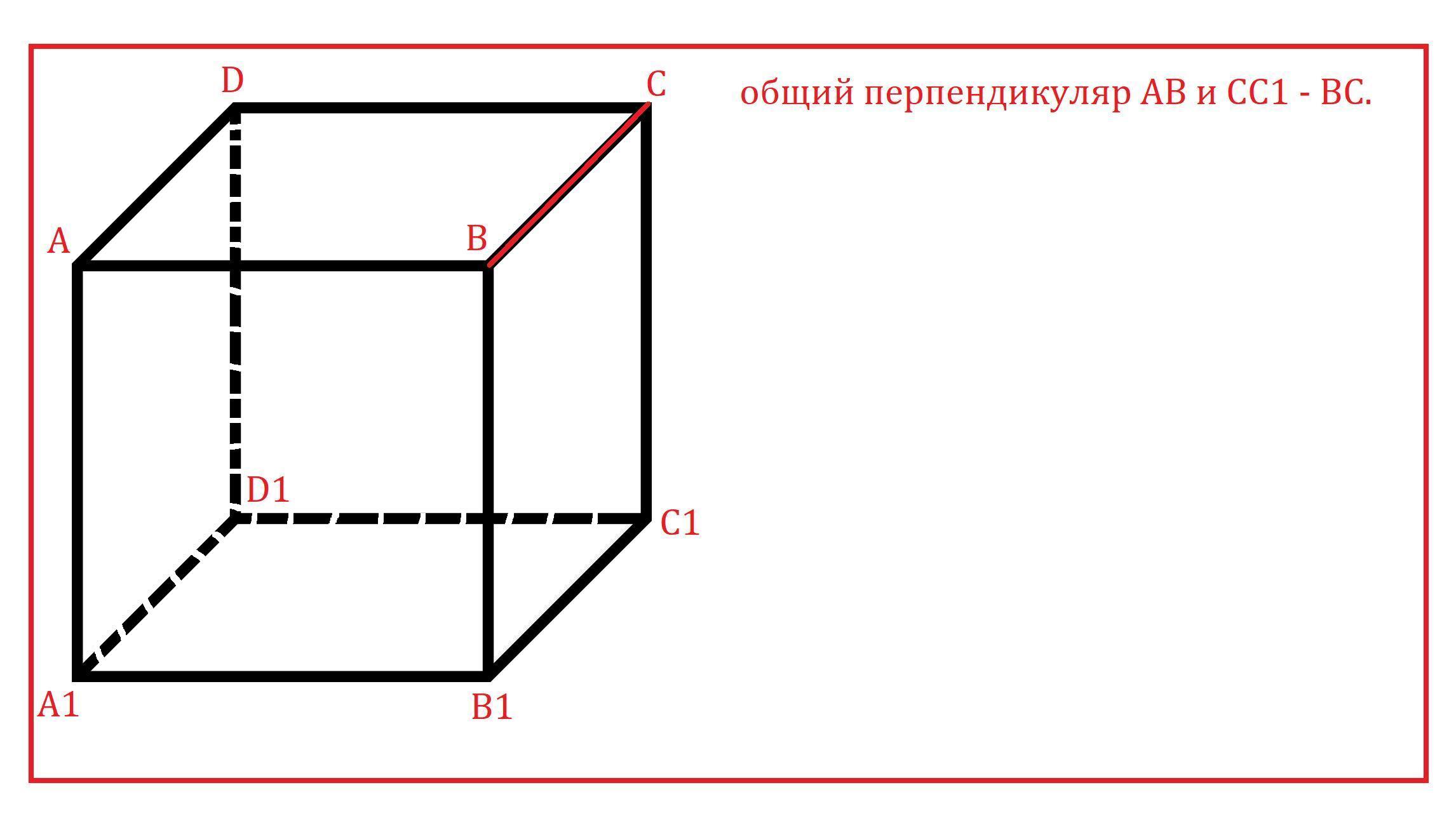
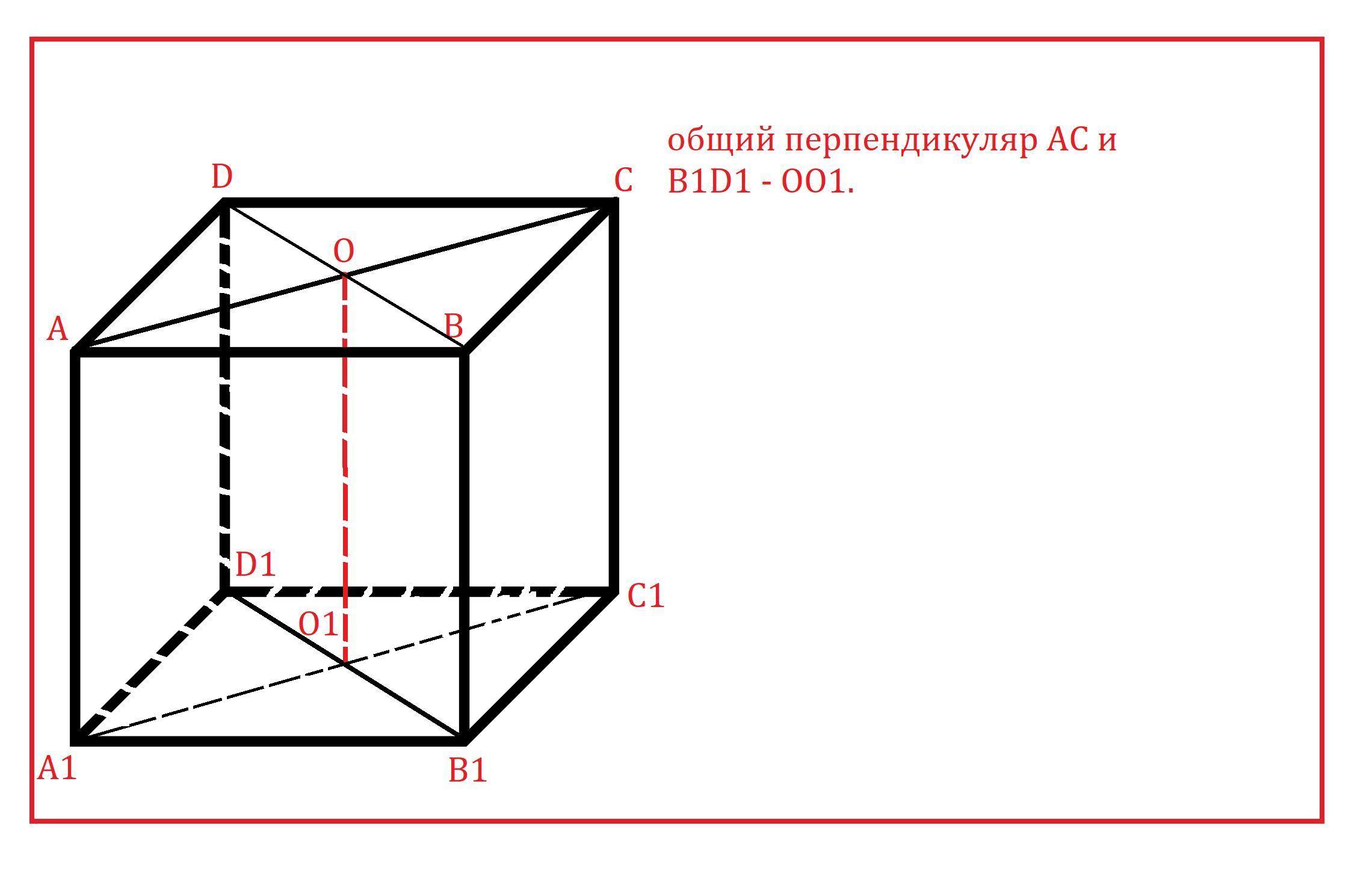
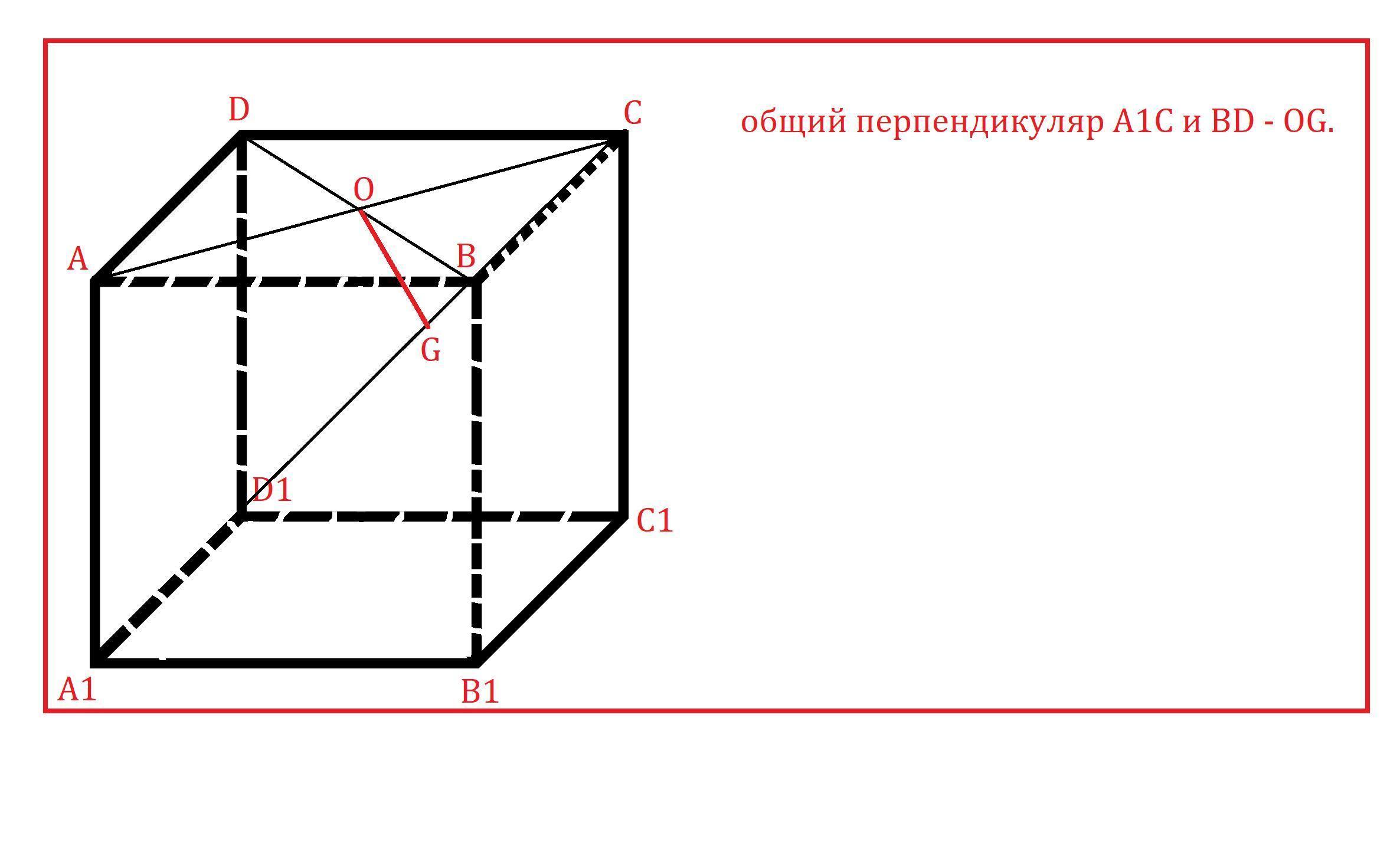
а) С1С и АВ; б) АС и В1D1; в*) ВD и А1С.

Answer 1

Ответ:

Всё в разделе "Объяснение"

Объяснение:

Проведём диагональ $B_1D$ прямоугольного параллелепипеда $ABCDA_1B_1C_1D_1.$

$A_1B_1 = 4$ см.

$B_1C_1 = 4$ см.

$C_1C = 2$ см.

$B_1D^{2} = A_1B_1^{2} + B_1C_1^{2} + CC_1^{2} =4^{2} + 4^{2} + 2^{2} = 36$

$B_1D = \sqrt{36} = 6$ см.

==================================================================

• Скрещивающиеся прямые - прямые, не лежащие в одной плоскости.

а) $AB \perp BC, CC_1 \perp BC,$ как стороны прямоугольника, значит $BC$ - общий перпендикуляр $AB$ и $CC_1.$

б) $O$ - точка пересечения диагоналей $AC$ и$BD.$

$O_{1}$ - точка пересечения диагоналей $A_1C_1$ и $B_1D_1.$

$AA_1C_1C$ - прямоугольник, значит $AO || A_1O_1, AO = OC$ и $A_1O_1 = O_1C_1$, по свойству диагоналей прямоугольника, тогда $AO = A_1O_1.$

$\Rightarrow AOO_1A_1$ - прямоугольник, значит $OO_1 || AA_1.$

$AA_1 \perp ABCD$ и $AA_1 \perp A_1B_1C_1D_1$ $\Rightarrow AA_1 \perp AC$ и $AA_1 \perp B_1D_1.$

$\Rightarrow$ общий перпендикуляр $AC$ и $B_1D_1$ - $OO_1.$

в) Через точку $O$ проведём в плоскости $(ACC_1)$ $OG \perp A_1C$, $BD \perp AC$ и $BD \perp CC_1 \Rightarrow BD\perp (ACC_1)$$\Rightarrow BD \perp OG$

$\Rightarrow$ общий перпендикуляр $A_1C$ и $BD$ - $OG.$