Предмет: Геометрия,
автор: 3618545
Срочноооо!!!! Дан прямоугольный параллелепипед АВСDА1В1С1D1. Найдите диагональ параллелепипеда, если его измерения таковы: 4 см, 5 см, 7 см. Постройте общий перпендикуляр скрещивающихся прямых: а) АD и C1C; б) D1D и В1C; в*) А1С и D1D.
Ответы
Автор ответа:
7
Ответ:
Всё в разделе "Объяснение".
Объяснение:
Проведём диагональ прямоугольного параллелепипеда
см.
см.
см.
============================================================
По свойству прямоугольного параллелепипеда,
см.
=========================================================
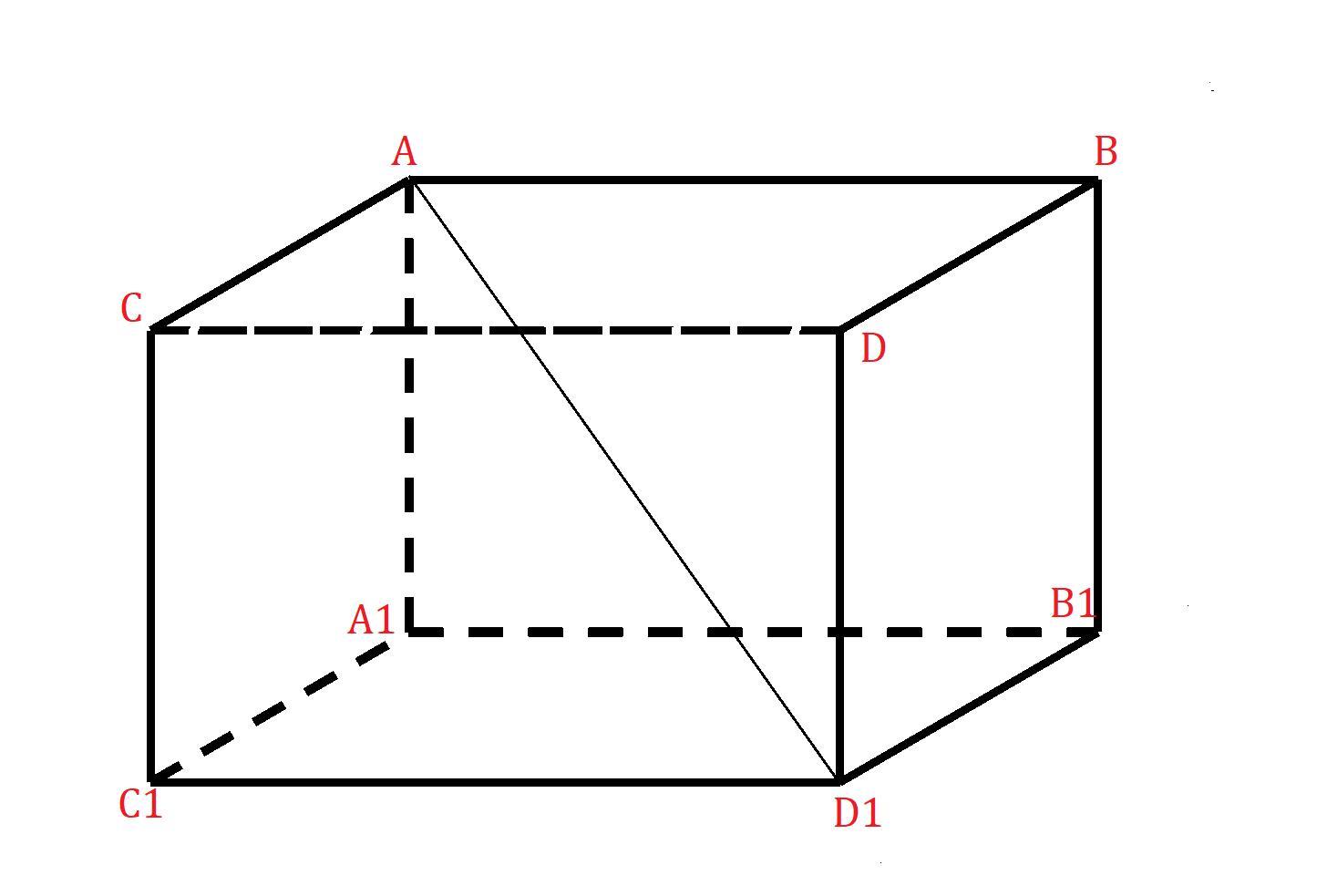
- Перекрещивающиеся прямые - прямые, которые не лежат в одной плоскости.
Проведём
.
Так как , по свойству прямоугольного параллелепипеда
общий перпендикуляр
и
-
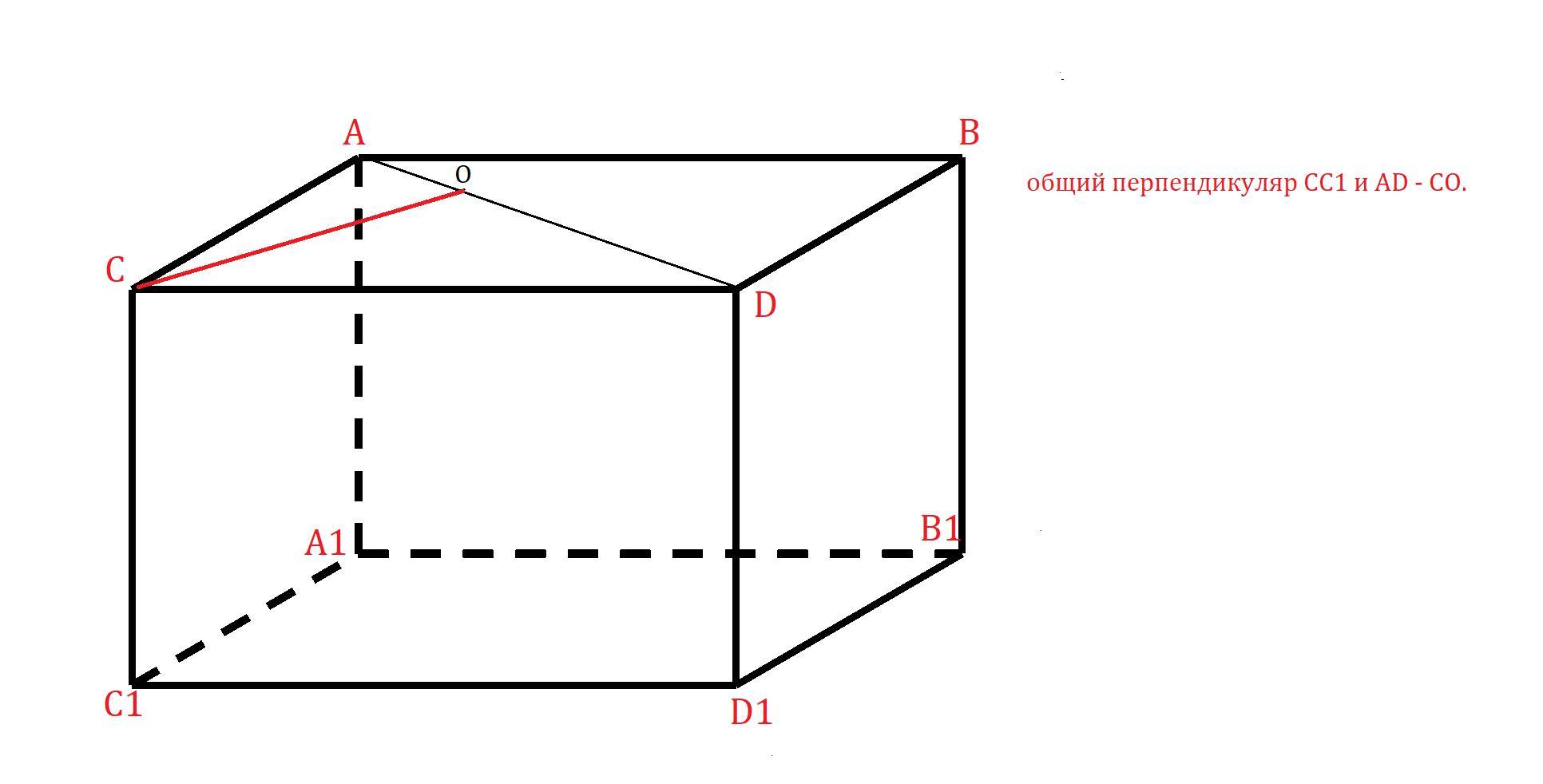
Проведём
.
Так как
общий перпендикуляр
и
-
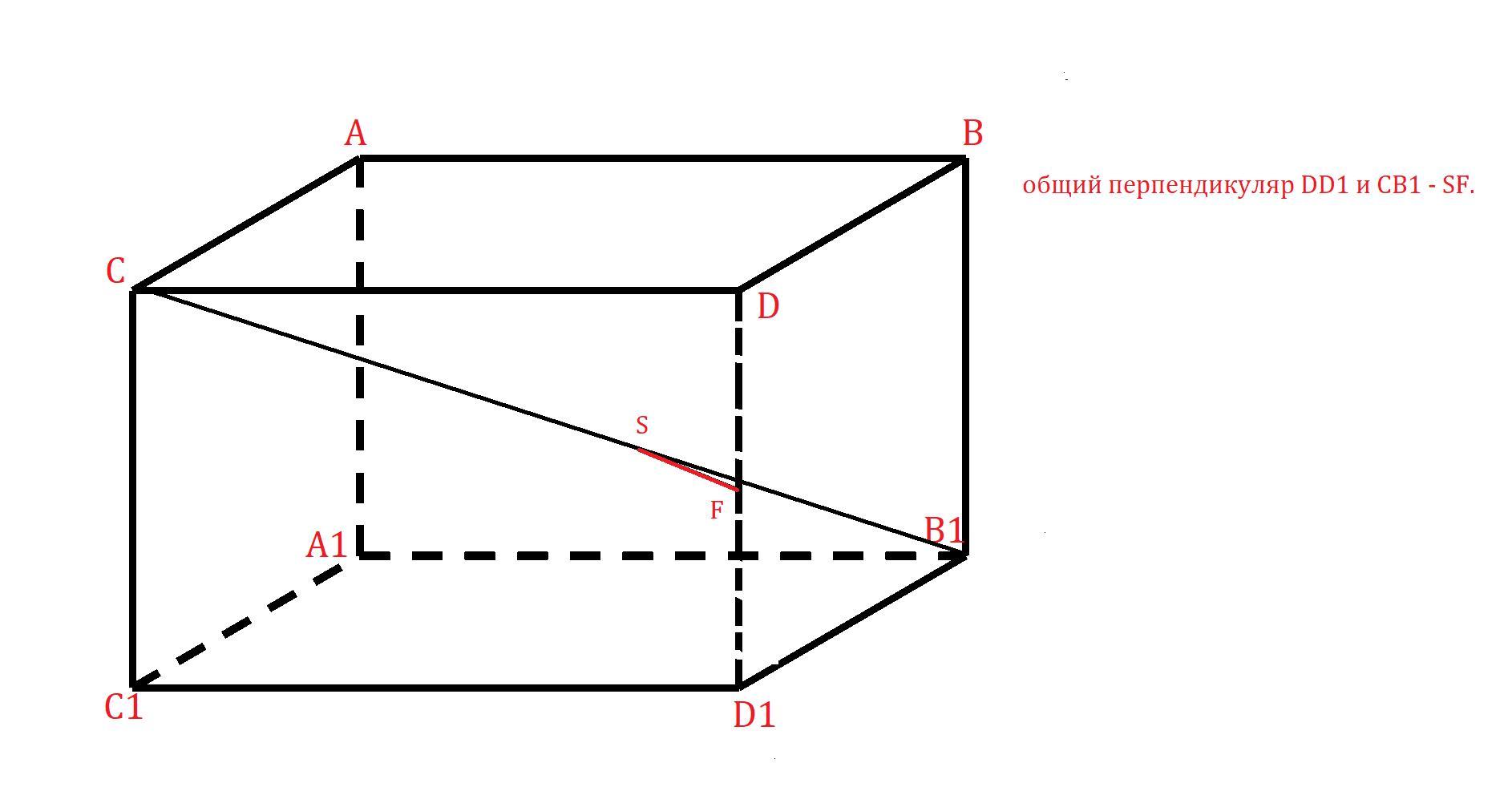
в) Общий перпендикуляр и
- расстояние между параллельными плоскостями
и
, в которых эти прямые лежат.
Поэтому общий перпендикуляр и
-
Приложения:
Похожие вопросы
Предмет: Литература,
автор: aleksandrabogovarova
Предмет: Химия,
автор: suleiman85555
Предмет: Математика,
автор: friendschannel048
Предмет: Информатика,
автор: Аноним
Предмет: Обществознание,
автор: Таня3785