Предмет: Алгебра,
автор: ШАТАНТРУБА
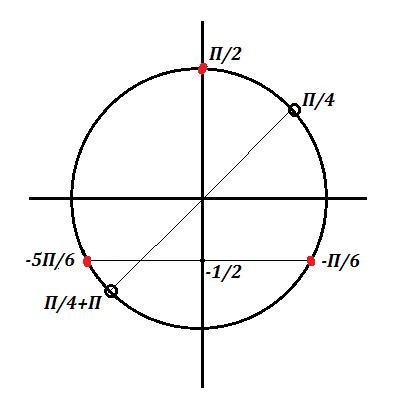
Решите уравнение.Непонятен момент с отбором корней,какие попадают в ОДЗ,а какие нет.
Приложения:

Ответы
Автор ответа:
0
Приложения:
Похожие вопросы
Предмет: Математика,
автор: zabrinakamalova87
Предмет: Английский язык,
автор: sofiya03122010
Предмет: Химия,
автор: playerfox67
Предмет: История,
автор: 10phil
Предмет: Алгебра,
автор: irkinexe