Question

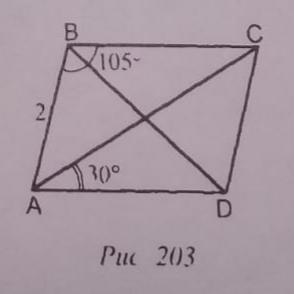
ABCD - параллелограмм. Найти: ВС

Answer 1

Дано: АВСD - параллелограмм.

<ABC = 105°, <CAD = 30°, AB = 2 ед.

Тогда <BAD = 180-105 = 75° (сумма углов, прилежащих к одной стороне параллелограмма, равна 180°), а <BAC=75-30 = 45°.

Опустим перпендикуляр ВН на диагональ АС. Тогда в прямоугольном треугольнике АВН острые углы равны по 45° и катеты

ВН = АН = √2 ед.

В треугольнике ВНС угол

<НВС = 105-45=60°, a <BCH = 30° (по сумме острых углов прямоугольного треугольника =90°).

Против угла 30° лежит катет, равный половине гипотенузы.  =>

ВС = 2√2 ед.