Помогите мне пожалуйста решить эту контрошку!!!!
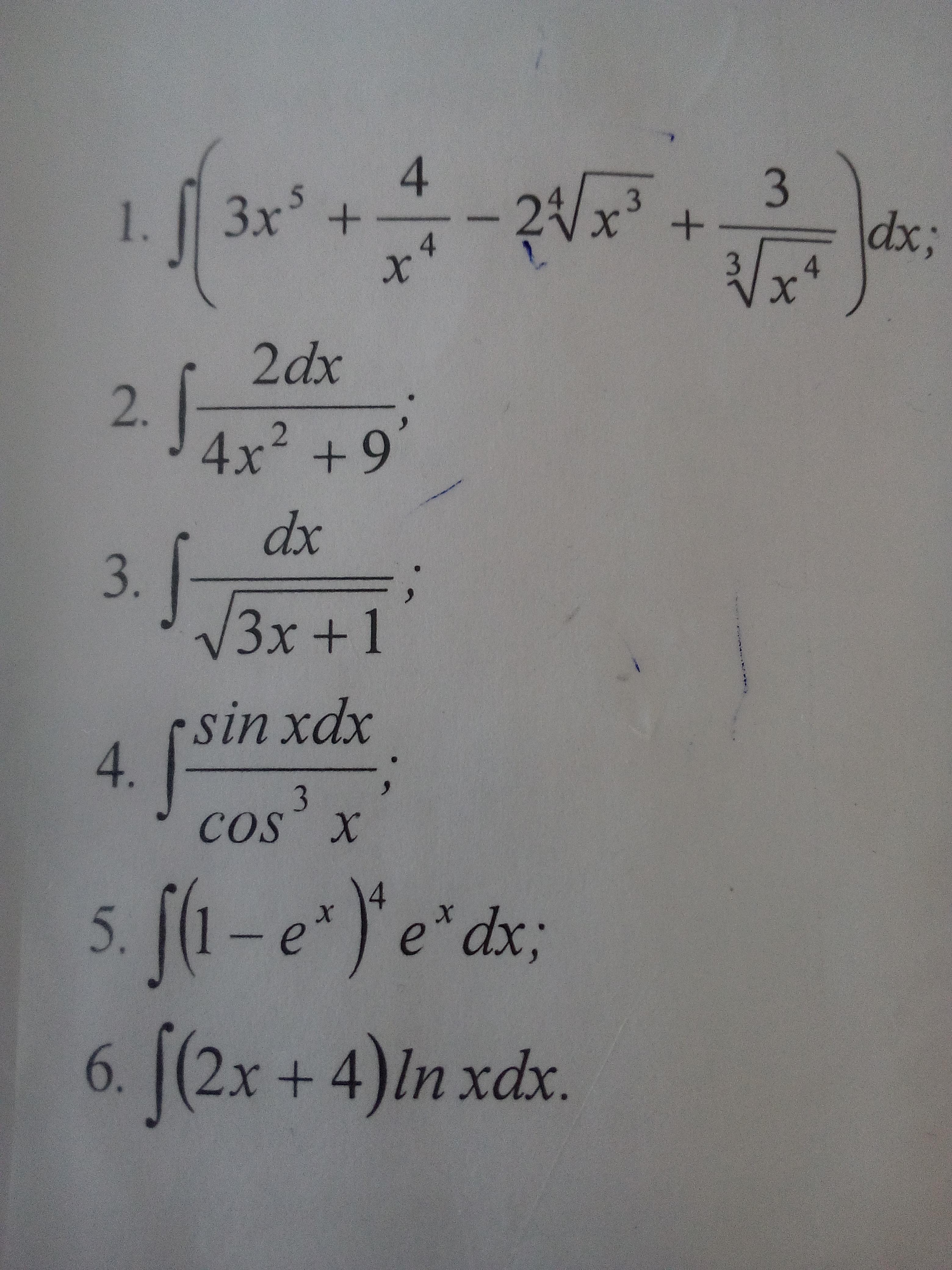
Ответы
Ответ:
Пошаговое объяснение:
1. Проинтегрируем каждое слагаемое отдельно, получим:
15х^4+4*(-4)*(x^(-5))-2*(3/4*x^-1/4)+3*3/4*x^1/4 + C
2. Вынесем 2 за знак интеграла, а оставшееся выражение проинтегрируем:
2* ㏑(4х^2+9)/8x+C
3. Проинтегрируем его, заметив, что это выражение похоже на производную от x^1/2, только без 2 в числителе, получим:
2*√(3х+1)/3+C
4. Разделим числитель и знаменатель и получим два слагаемого:
tgx + 1/cos^2
Проинтегрируем его:
(-㏑(cosx)+tgx)+C
5. Разложим первый множитель выражение с помощью бинома Ньютона, получим:
(1+4(e^x)+6(e^x)^2+4(e^x)^3+(e^x)^4)e^x
Проинтегрировав это выражение получим:
8e^2x+18e^3x+16e^4x+5e^5x
6. Избавившийся от скобок(умножением) и проинтегрировав получим:
-x^2/2+x(x+4)*ln(x)-4x
Здесь используется способ интегрирование по частям