Предмет: Алгебра,
автор: Ilya1118
428 а плиииииииииииииииииз
Приложения:
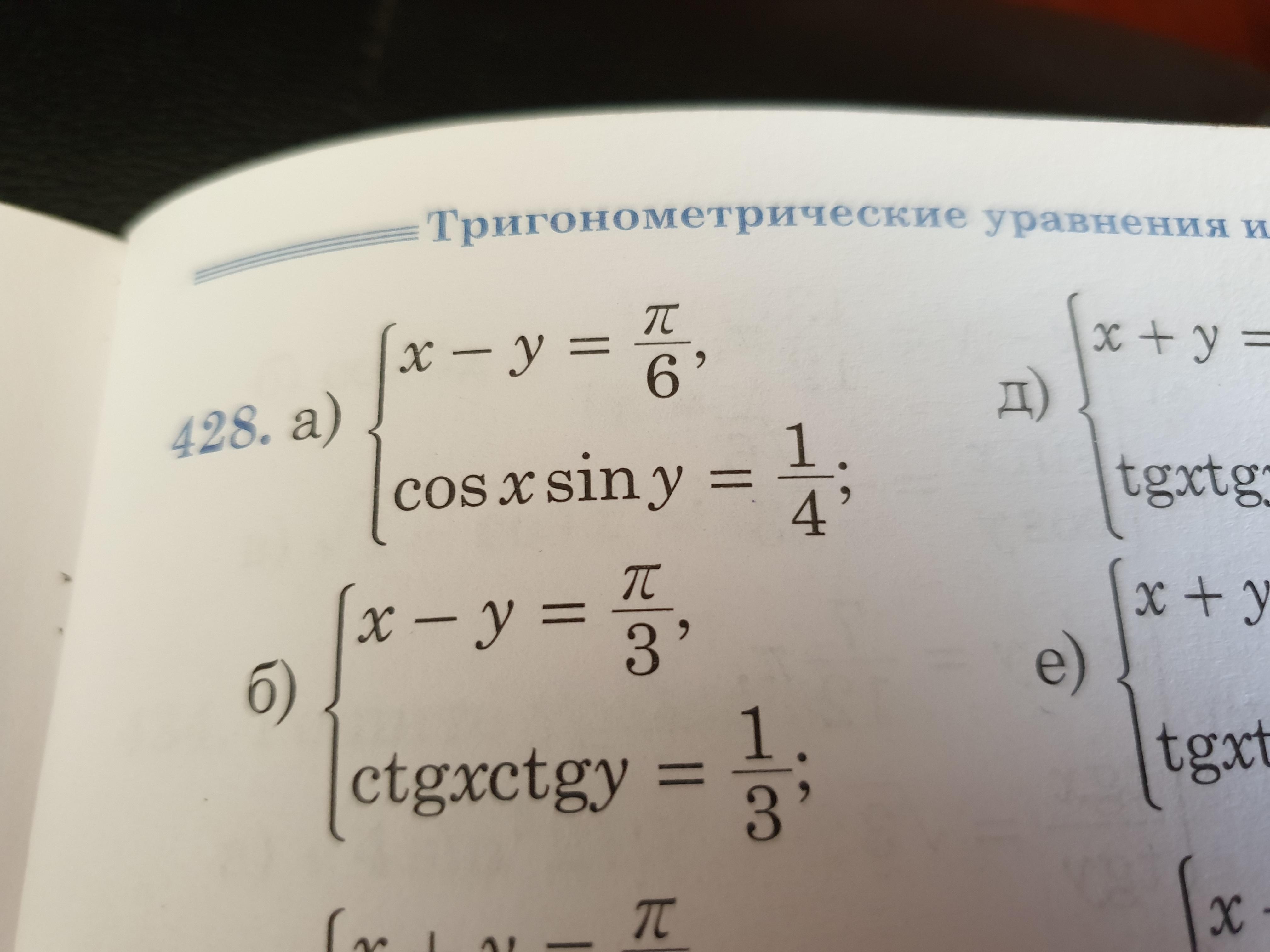
Ответы
Автор ответа:
3
Ответ:
Похожие вопросы
Предмет: История,
автор: vadimbazarov420
Предмет: География,
автор: artemiikislov
Предмет: Английский язык,
автор: smirnovapolina160120
Предмет: Математика,
автор: Anastasia012007