Question

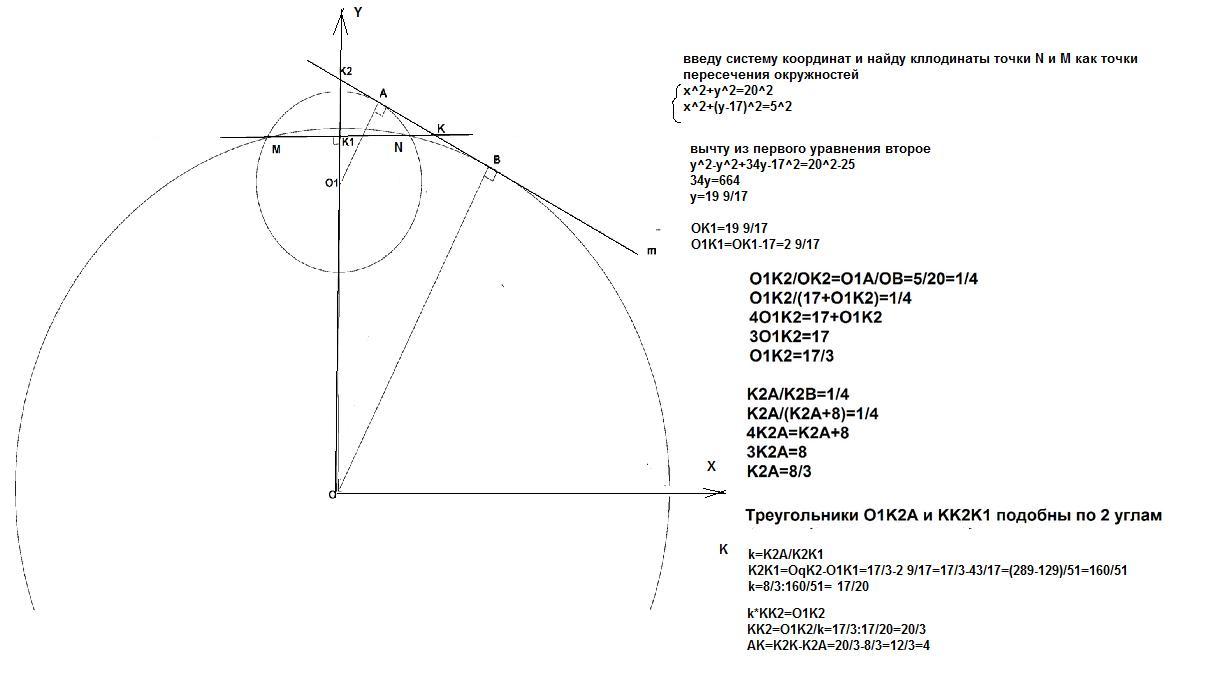
Красивая задачка: Даны две окружности, которые пересекаются в точках M и N. Прямая m проходит по касательной в точках A и B этих окружностей. Прямая MN пересекает AB в точке К.
а) Докажите, что точка персечений медиан треугольника АВМ лежит на прямой MN.
б) найдите АК, если известно, что расстояние между центрами окружностей равно 17, а радиусы равны 20 и 5.​

Answer 1

.а)AB=8(по т пифагора)

тогда если АК=4, то МК-медиана треугольника АМВ,следовательно на ней лежит точка пересечения медиан треугольника, а значит и на MN лежит эта точка

(NK<MK/3)