Предмет: Геометрия,
автор: LerroyJay
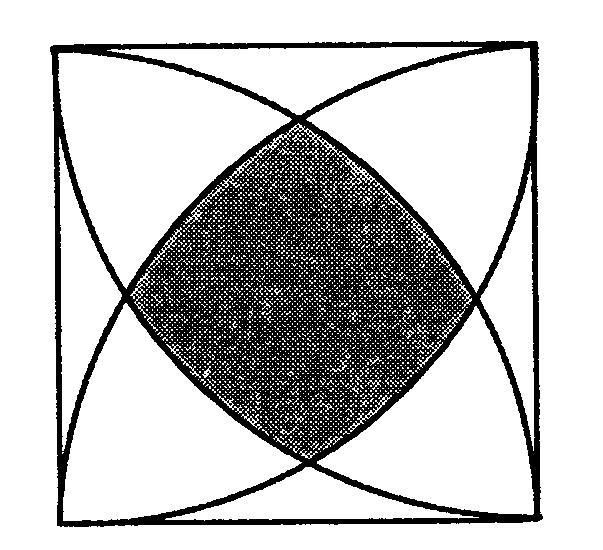
Сторона квадрата равна α. Найти площадь закрашенной области.
Приложения:
Ответы
Автор ответа:
4
Разделим искомую фигуру на квадрат со стороной x и четыре сегмента окружности, радиус a, угол 30.
По теореме косинусов
x^2= 2a^2 -2a^2 cos30 = a^2(2-√3)
Площадь сегмента, радиус a, угол 30
Sсег= пa^2 30/360 -a^2 sin30/2 = a^2(п/12 -1/4)
S= x^2 +4Sсег = a^2(2-√3) +a^2(п/3 -1) = a^2(1 +п/3 -√3)
Приложения:
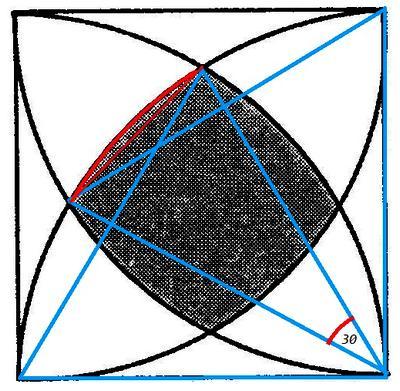
siestarjoki:
Радиусы образуют на сторонах квадрата равносторонние треугольники. 90-60=30.
Вычитаем из прямого угла два по 30 - остается 30.
Надо, наверное, переделать рисунок.
Есть задача о трисекции прямого угла.
i.imgur.com/ic5iGyP.png
Похожие вопросы
Предмет: Математика,
автор: basistijartem224
Предмет: Английский язык,
автор: aleklandrazobkova
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: яна1117
Предмет: Математика,
автор: hollymbolly