Предмет: Алгебра,
автор: kseniarud1
Помогите решить, в ответе -2, нужно решение.
Приложения:
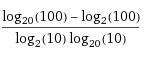
Ответы
Автор ответа:
1
kseniarud1:
Верно, спасибо. Закрыто.
Похожие вопросы
Предмет: Математика,
автор: KitsuSudzuki
Предмет: Физика,
автор: Zhdanov2007
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: vikusha899
Предмет: Литература,
автор: Gayane0987