Предмет: Геометрия,
автор: oksanapodgornova
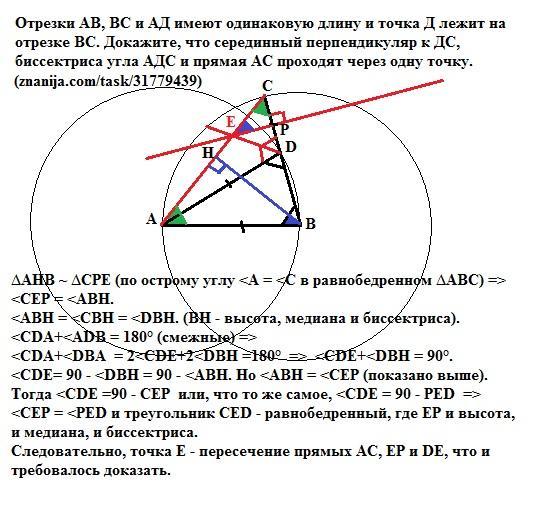
Отрезки АВ, ВС и АД имеют одинаковую длину и точка Д лежит на отрезке ВС. Докажите, что серединный перпендикуляр к ДС, биссектриса угла АДС и прямая АС проходят через одну точку
Hrisula:
Фигура - равнобедренный треугольник АСD, в котором AC=AD и отрезок СВ=продолжение CD и равно АВ=АD
Ответы
Автор ответа:
3
∆АНВ ~ ∆CPE (по острому углу <A = <C в равнобедренном ∆АВС) =>
<CEP = <ABH.
<ABH = <CBH = <DBH. (ВН - высота, медиана и биссектриса).
<CDA+<ADB = 180° (смежные) =>
<CDA+<DBA = 2<CDE+2<DBH =180° => <CDE+<DBH = 90°.
<CDE= 90 - <DBH = 90 - <ABH. Но <ABH = <CEP (показано выше).
Тогда <CDE =90 - <CEP или <CEP = 90 - <CDE.
В прямоугольном треугольнике PDE
PED = 90 - <CDE =>
<CEP = <PED и треугольник СED - равнобедренный, где ЕР и высота, и медиана, и биссектриса.
Следовательно, точка Е - пересечение прямых АС, ЕР и DE, что и требовалось доказать.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: bebrakenkeneki
Предмет: История,
автор: valeriadanchuk23
Предмет: Информатика,
автор: djenburunduk
Предмет: Математика,
автор: робот777
Предмет: Математика,
автор: белова4444