помогите, заранее спасибо... Буду очень благодарен!)
Ответы
Рассмотрим ΔCAD - прямоугольный
CD = 2AD - гипотенуза (катет, лежащий напротив угла в 30°, равен половине гипотенузы)
По теореме Пифагора
(2AD)² = AD² + AC²
(2AD)² = AD² + 18²
4AD² = AD² + 324
4AD² - AD² = 324
3AD² = 324
AD² = 324/3 = 108
AD = √108 = √(36 *3) = 6√3
Площадь параллелограмма равна произведению его основания на высоту, проведенную к этому основанию
S = 6√3 * 18 = 108√3
Ответ: S = 108√3
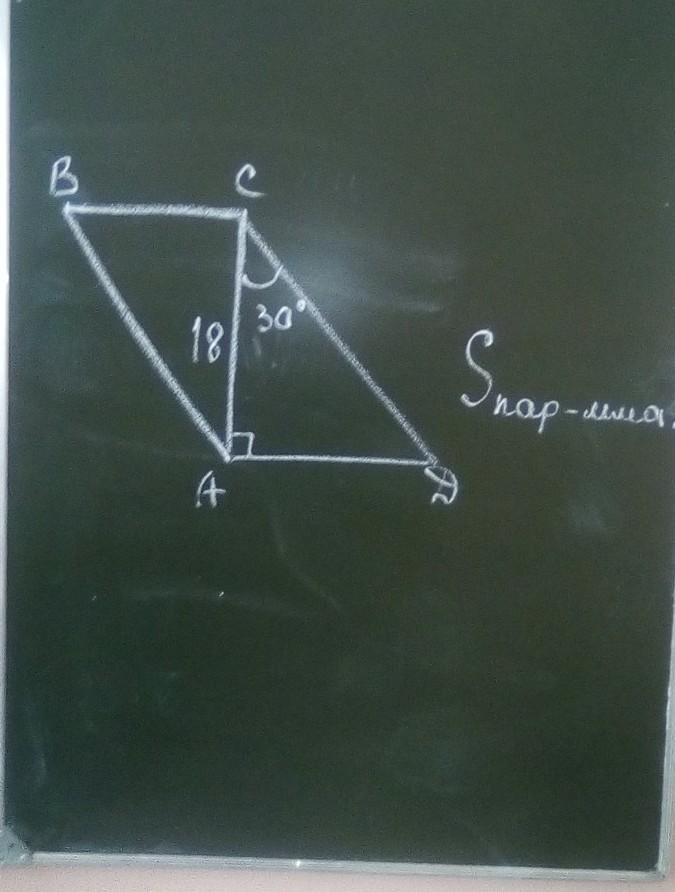
В параллелограмме АВСD диагональ АС перпендикулярна стороне АD и образует со стороной CD угол 30°. Найдите площадь параллелограмма.
Площадь параллелограмма равна произведению длин высоты и стороны, к которой проведена. S(ABCD)=CA•AD.
Треугольник САD прямоугольный, угол САD=90°, угол АСD=30°. АD=CA•tg30°=18•1/√3. AD= 6√3. S(ABCD)=18•6√3=108√3(ед. площади)