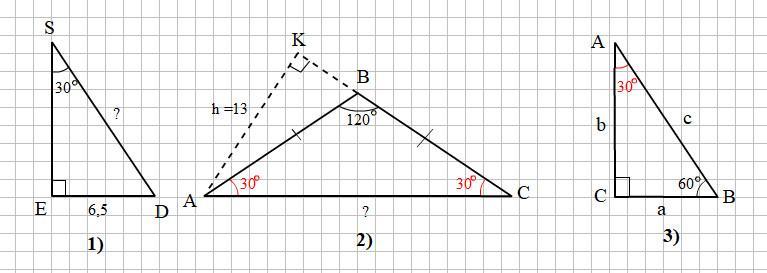
1)В прямоугольном треугольнике des угол s равен 30°,угол E равен 90°.Найдите гипотенузу DS этого треугольника если катет DE равен 6,5 см
2)Угол при вершине равнобедренного треугольника равен 120° высота, проведенная к боковой стороне равна 13 см. Найдите основание этого треугольника
3)Один из углов прямоугольного треугольника равен 60 градусов сумма гипотенузы и меньшего из катетов равны 21 см .Найдите гипотенузу
Ответы
Ответ:
1) 13 см; 2) 26 см; 3) 14 см;
Объяснение:
Смотри прикреплённый рисунок.
1) DS - гипотенуза прямоугольного Δ DES
Катет DE лежит против ∠S = 30°, поэтому DE = 0,5 DS
Следовательно, DS = 2 · DE = 2 · 6.5 см = 13 см.
2) В равнобедренном Δ АВС, угол при вершине ∠В = 120°.
По свойству углов треугольника углы при основании равны
∠А = ∠ С = 0,5 · (180° - 120°) = 30°.
В прямоугольном ΔАКС АС является гипотенузой, а катет АК = 13 см лежит против ∠С = 30°, поэтому АС = 2 · АК = 2 · 13см = 26 см.
3) В прямоугольном ΔАВС (∠С = 90°; ∠В = 60°) меньший острый угол
∠А = 90° - ∠В = 90° - 60° = 30°.
Введём обозначения: ВС = а - меньший катет; АВ = с - гипотенуза.
Катет ВС = а лежит против ∠А = 30°, поэтому катет ВС равен половине гипотенузы АВ = с
а = 0,5с
По условию с + а = 21 см
0,5с + с = 21
1,5с = 21
с = 14 (см)