Помогите решить 2.112 и 2.114

Ответы
2.112.
1) A и C уже принадлежат плоскости (ABC), опустим перпендикуляр из B₁ на плоскость (ABC) т.к. мы работаем с кубом, то это будет точка B. Значит нам надо найти площадь треугольника ABC, его площадь равна половине площадь квадрата ABCD, а именно
см²
2) A и C уже принадлежат плоскости (AA₁C₁), остаётся опустить перпендикуляр из B₁ на эту плоскость. A₁O=OC₁(O∈A₁C₁) O это и есть проекция. Докажем это. B₁O перпендикулярно A₁C₁ т.к. это медиана в равнобедренном треугольнике (она же и высота). AA₁⊥A₁B₁,A₁C₁--> AA₁⊥(A₁B₁C₁)-->AA₁⊥B₁O. B₁O⊥AA₁,A₁C₁-->B₁O⊥(AA₁C₁), доказано.
Надо найти площадь треугольника ACO, его высота равна AA₁=8см, т.к. это куб, рёбра параллельны и вообще всё идеально. AC=8√2см как диагональ квадрата со стороной 8см. Площадь равна высота на сторону и полам.
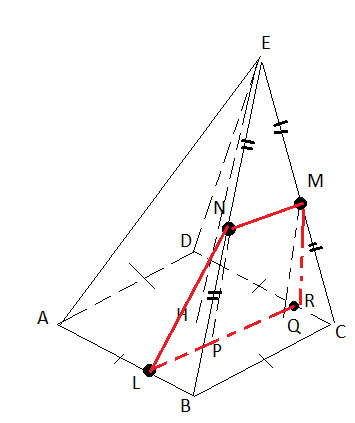
2.114.
Зададим правильную четырёхугольную пирамиду. ABCD-квадрат; EH⊥(ABC)
Отметим точки: ME=MC; NE=NB.
α-наша плоскость (;
α⊥(ABC)-->α║EH. Проводим NP║EH в плоскости (BEH) и MQ║EH в (ECH). Значит P∈NB, Q∈HC. Этого в принципе достаточно чтобы найти P, Q на (ABC), но лучше по точнее.
Эти точки принадлежат α. Так же MN средняя линия ΔEBC значит MN║BC. PQ║MN как след MN на (ABC) от α--> PQ║BC, рисуем эту параллельную линию (Суть в том, что не понятно как именно упадут P и Q, но мы знаем, что PQ точно параллельна BC). Ну а дальше соединяем точки, всё просто.
Сечение плоскость α, это LRMN.
У меня не очень параллельно получалось, попробуй лучше.