решите все..........
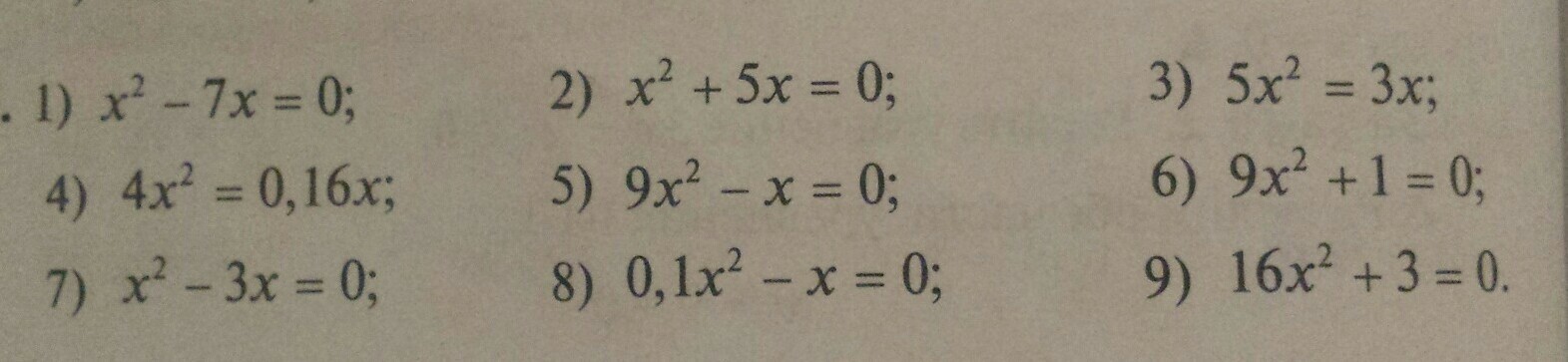
Ответы
1)
вспоминаем любимый Дискриминант.
D = - 4ac;
D = = 49
Потом решение.
(-b ± √D) / 2
2)D = 25
3)
D = 9
4)
D =
5) D = 1
[/tex]
6) D =
Так как D должен быть , то у уравнения нет корней.
7) D = 9
8)
D = 100
9) аналогично 6 только другие числа.
D = -4 *3 * 16 = -192
нет корней.
Вы уже исправили, вроде бы
Когда произведения чего-то равно нулю? Когда одно из рано нулю, а другое существует (не нарушаются правила: делит на ноль нельзя, корень чёт ст. из отрицательного числа брать нельзя, квадрат не(=)отрицательное).
В общем можно записать так: Ответ: x={0;7}
2)
Ответ: x={-5;0}
3)
Ответ: x={0;0.6}
4)
Ответ: x={0;0.04}
5)
Ответ: x={0;1/9}
6)
Квадрат не может равняться отрицательному числу.
Ответ: нет решений.
7)
Ответ: x={0;3}
8)
Ответ: x={0;10}
9)
Ответ: нет решений.
Это были не полные квадратные уравнения, их суть в том что, либо b, либо c равны нулю:
В таких случая не ищут дискриминант, а решают используя свойства квадрата и 0*a=0