Предмет: Алгебра,
автор: RiosLorenzoAlexandra
Помогите, пожалуйста, 60 баллов!!!
Приложения:
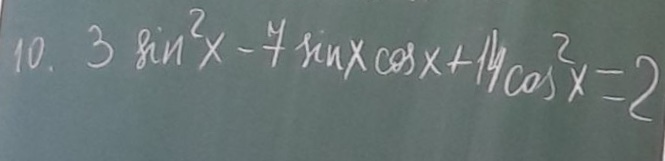
Ответы
Автор ответа:
1
Автор ответа:
1
3sin²x-7sinxcosx+14cos²x-2(sin²x+cos²x)=0
sin²x-7sinxcosx+12cos²x=0
:cos²x≠0
tg²x-7tgx+12=0
tgx=t
t²-7t+12=0
D=49-48=1
t=(7±1)/2
t1=4
t2=3
tgx=4;x=arctg4+πk
tgx=3;x=arctg3+πk;k€Z
sin²x-7sinxcosx+12cos²x=0
:cos²x≠0
tg²x-7tgx+12=0
tgx=t
t²-7t+12=0
D=49-48=1
t=(7±1)/2
t1=4
t2=3
tgx=4;x=arctg4+πk
tgx=3;x=arctg3+πk;k€Z
Похожие вопросы
Предмет: Математика,
автор: snezanasnezana889
Предмет: Английский язык,
автор: coolweirdnormal
Предмет: Математика,
автор: Nina091212
Предмет: Химия,
автор: volkova234
Предмет: Математика,
автор: Nasi2503