Предмет: Математика,
автор: Biryi
Можно пожалуйста с объяснением
Приложения:
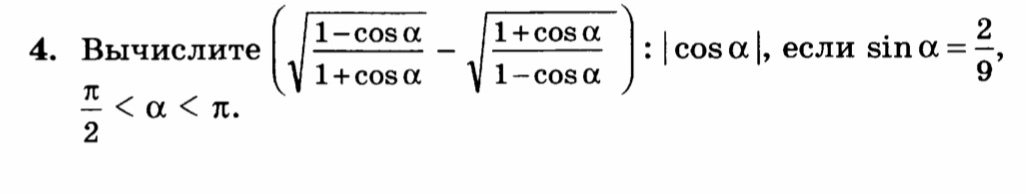
Ответы
Автор ответа:
1
Ответ: 9
Решение.
1. Для начала нужно через синус выразить косинус с помощью основного тригонометрического тождества, получим:
Чтобы определить знак косинуса нужно посмотреть к какому промежутку принадлежит угол альфа, в нашем случае от
до
В таком диапазоне значение синуса отрицательно, значит знак перед корнем будет стоять минус. Подставим значение синуса и получим следующее значение косинуса:
Подставляет это выражение в выше указанное преобразует и вычисляем, только обратите на модуль в знаменателе, когда будете его вычислять минус уйдёт. В итоге получится следующий ответ: 9
Похожие вопросы
Предмет: Алгебра,
автор: zetdefect
Предмет: Химия,
автор: korovecoleksandr2
Предмет: Литература,
автор: tapokstalina908
Предмет: Математика,
автор: биби17
Предмет: Алгебра,
автор: sh0ckerz77141