Question

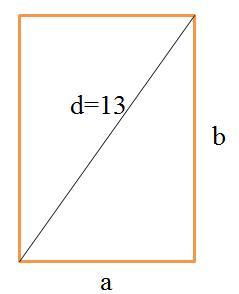
Длина диагонали прямоугольника равна 13, а его площадь 60. Найдите стороны прямоугольника

Answer 1

Стороны прямоугольника
12 и 5 см.

Answer 2

Пусть стороны прямоугольника равны a и b сантиметров.
Тогда из первого условия следует: диагональ — гипотенуза, стороны прямоугольника — катеты, т.е.
a^2+b^2=13^2=169
Из второго условия следует: a*b=60

Т.е. получили систему с двумя неизвестными. Выразим из второго уравнения b, подставим первое, получим уравнение с одним неизвестным:
b=60/a
a^2+3600/a^2=169
a^4-169a^2+3600=0
пусть t=a^2, тогда
t^2-169t+3600=0
D=169^2-4*3600=28561-14400=14161
корень из D = 119
т.е. t_1 = (169+119)/2=144
t_2=(169-119)/2=25
находим теперь a:
a^2=144 => a=12
a^2=25 => a=5

Теперь находим b:
b=60/12=5 при a=12
b=60/5=12 при a=5
То есть стороны прямоугольника равны 5 и 12.

Answer 3

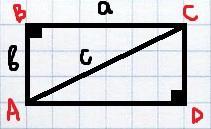
Обозначим длину прямоугольника как а, ширину прямоугольника как b, и диагональ как c.

Рассмотрим ΔABC: ∠B=90° ⇒ ΔABC - прямоугольный; a,b - катеты, c - гипотенуза

т. Пифагора гласит:

a² + b² = c²

a² + b² = 13²

a² + b² = 169

А площадь прямоугольника находится по формуле:

S = a * b

a * b = 60

Составим систему уравнений и решим методом подстановки.

$left { {{a^2+b^2=169} atop {ab=60}} right. Longrightarrow left { {{a^2+b^2=169} atop {a=frac{60}{b}}} right.$

$(frac{60}{b})^2+b^2=169\\frac{3600}{b^2}+b^2=169|*b^2\\3600+b^4=169b^2\b^4-169b^2+3600=0$

Вводим новую переменную.

b² = t - новая переменная.

$t^2-169t+3600=0\D=(-169)^2-4*1*3600=28561-14400=14161\sqrt{14161}=119\\t_1=frac{169-119}{2}=25\\t_2=frac{169+119}{2}=144$

b² = t

b² = 25 или b² = 144

b₁ = 5; b₂=-5; b₃=12; b₄=-12

Т.к. сторона не может быть отрицательна, то -5 и -12 не подходят.

a * b = 60

a₁ * 5 = 60

a₁ = 12

a₂ * 12 = 60

a₂ = 5

⇒ Стороны прямоугольника равны 5 см и 12 см.

Ответ: 5 см; 12 см

Answer 4

Ответ:

5 и 12

Пошаговое объяснение:

Пусть стороны прямоугольника a и b, диагональ d. Площадь прямоугольника равна: S = a · b. По условию a · b = 60, а диагональ d = 13.

Диагональ делит прямоугольник на два прямоугольных треугольника и поэтому верна теорема Пифагора: d² = a² + b².

На основе условий задачи получаем систему уравнений:

$left { {a^{2} +b^{2} =13^{2} } atop {a*b=60}} right.$

Второе уравнение умножим на 2 и прибавим к первому:

$left { {a^{2} +2*a*b+b^{2} =169+120 } atop {a*b=60}} right.\\left { {(a+b)^{2} =289 } atop {a*b=60}}$

a и b стороны прямоугольника и поэтому a+b>0:

$left { {a+b =17 } atop {a*b=60}}$

Решаем систему методом  подстановки:

$left { {b =17-a } atop {a*(17-a)=60}}$

a²-17·a+60=0

D=(-17)²-4·1·60=259-240=49=7²

a₁=(17-7)/2=10/2=5, тогда b₁ =17-5=12

a₂=(17+7)/2=24/2=12, тогда b₂ =17-12=5.

Отсюда, ответом будут 5 и 12.