Предмет: Алгебра,
автор: marisichka
20 БАЛЛОВ, производная сложной функции
Приложения:
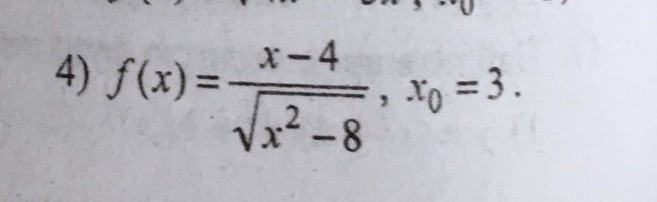
Ответы
Автор ответа:
1
marisichka:
разве формула такая?
там же должно быть,чтобы от числителя отнимали знаменатель + там еще производная сложной функции, вы уверены, что там так?
от числителя не отнимают знаменатель !!! Смотри формулу производной дроби !!!
написала тебе формулу...
теперь поняла, спасибо
Похожие вопросы
Предмет: Математика,
автор: andreevav539
Предмет: Информатика,
автор: Ublyd0k
Предмет: Математика,
автор: kotovsergej625
Предмет: Алгебра,
автор: ShaggyEggs
Предмет: Алгебра,
автор: polinavinnikova