Предмет: Математика,
автор: gadziverdievtimur7
В одной из клеток доски 5×5(5 строк, 5 столбцов) стоит фишка. За один ход можно передвинуть её на соседнюю по углу клетку, либо на одну клетку вправо, либо на одну клетку влево. Какое наибольшее количество ходов можно сделать так, чтобы фишка не побывала ни в какой клетке дважды?Заранее спасибо
Ответы
Автор ответа:
1
Если рассмотрим стандартный вариант, и не будем усложнять задачу то естественно ответ 5. Ставим фишку в самый левый или самый правый столбик и двигаем ее по строке. Столбцов 5 , то ответ:5 . Если задача на логику то можно предположить что доску можно крутить и тогда ответом будет число 40. Я ходил фишкой спиралью. Так мы получим максимальное число ходов. Она остановится в центре. Пишу оба варианта , потому что задача вроде подозрительно легкая. Может быть олимпиадного уровня
Приложения:
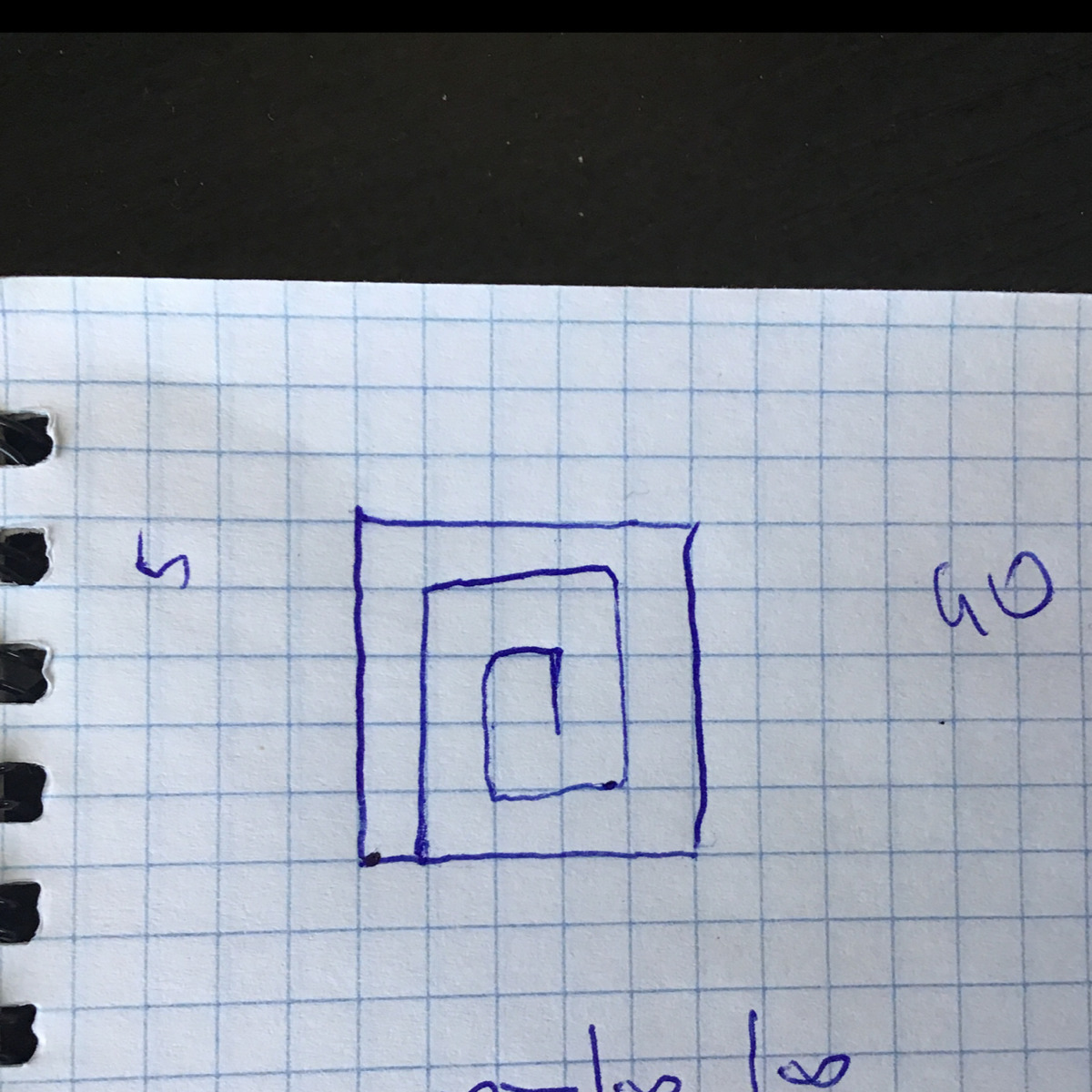
kostenka177:
Я там нечаянно провёл лишний отрезок, если присмотреться. Но я его не считал, так что не обращайте внимания
Сори ответ 35, если спиралью идти. Я пересчитал
А как?
Просто я только вчера зарегестрировался
IOS
Похожие вопросы
Предмет: Английский язык,
автор: volkovael583
Предмет: Окружающий мир,
автор: mflm
Предмет: Алгебра,
автор: justtty0ns0
Предмет: Химия,
автор: dashamilerr
Предмет: Геометрия,
автор: Artem007111