Предмет: Алгебра,
автор: simovskaya
Решите уравнение 1+x+x^2+...x^99=0. Заранее благодарю
Приложения:
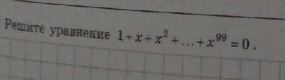
Ответы
Автор ответа:
9
1+x+x^2+..+x^99 =
= 1+x+x^2+x^3+x^4+x^5...+x^98+x^99 =
= 1+x+x^2(1+x)+x^4(1+x)...+x^98(1+x) =
= (1+x)(1+x^2+x^4+...+x^98) = 0
Данное уравнение равносильно двум уравнениям:
1+x=0, откуда х = -1
1+x^2+x^4+...+x^98 = 0 - решений нет, так как все степени чётные
Исходное уравнение имеет только один корень: х = -1
Похожие вопросы
Предмет: Литература,
автор: Аноним
Предмет: История,
автор: kirillharkovskij
Предмет: Геометрия,
автор: chechil12345678910
Предмет: Математика,
автор: mashareyrey201