Question

Помогите пожалуйста решить:
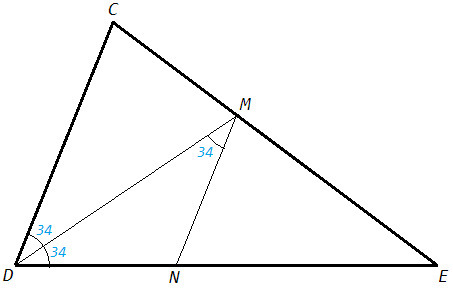
Дан треугольник CDE: угол CDE=68 градусов. DM биссектриса угла CDE. т. М лежит на стороне CE. Проведите MN//CD, т.N-на стороне DE. Выделите треугольник DMN и найдите его углы: угол MDN, угол DNM, угол NMD

Answer 1

∠CDM=∠NDM=∠CDN/2 =34° (DM - биссектриса ∠CDN)

∠DNM=180°-∠CDN =180°-68°=112° (∠CDN, ∠DNM - внутренние односторонние при CD||MN)

∠NMD=∠CDM =34° (∠CDM, ∠NMD - накрест лежащие при CD||MN)