Question

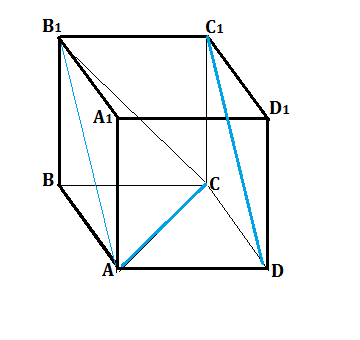
Дан куб ABCDA1B1C1D1.
Найдите угол между прямыми  AC и DC1.

Answer 1

СD1 - диагональ грани DCC1D1  куба. 
АС лежит в плоскости  грани АВСD и является ее диагональю.   
DС1 не лежит в той же  плоскости и пересекает ее в точке, не принадлежащей АС.  Если одна из двух прямых лежит в плоскости, а другая пересекает эту плоскость в точке, не принадлежащей первой прямой, то эти прямые скрещиваются. ⇒ 
прямые DC1 и AC - скрещивающиеся.
Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, соответственно параллельными данным.  Проведем в грани АВВ1А1 диагональ АВ1||DC1  и в грани ВСС1В1  диагональ СВ1 Все грани куба квадраты и равны между собой. 
АС=АВ1=СВ1  как диагонали равных квадратов. 
Треугольник АСВ1 - равносторонний, и углы между его сторонами равны 60º⇒
Угол между ДС1 и АС=углу между АВ1 и АС и равен 60º