Предмет: Алгебра,
автор: eQbiX
Решите неравенство с модулем
Приложения:
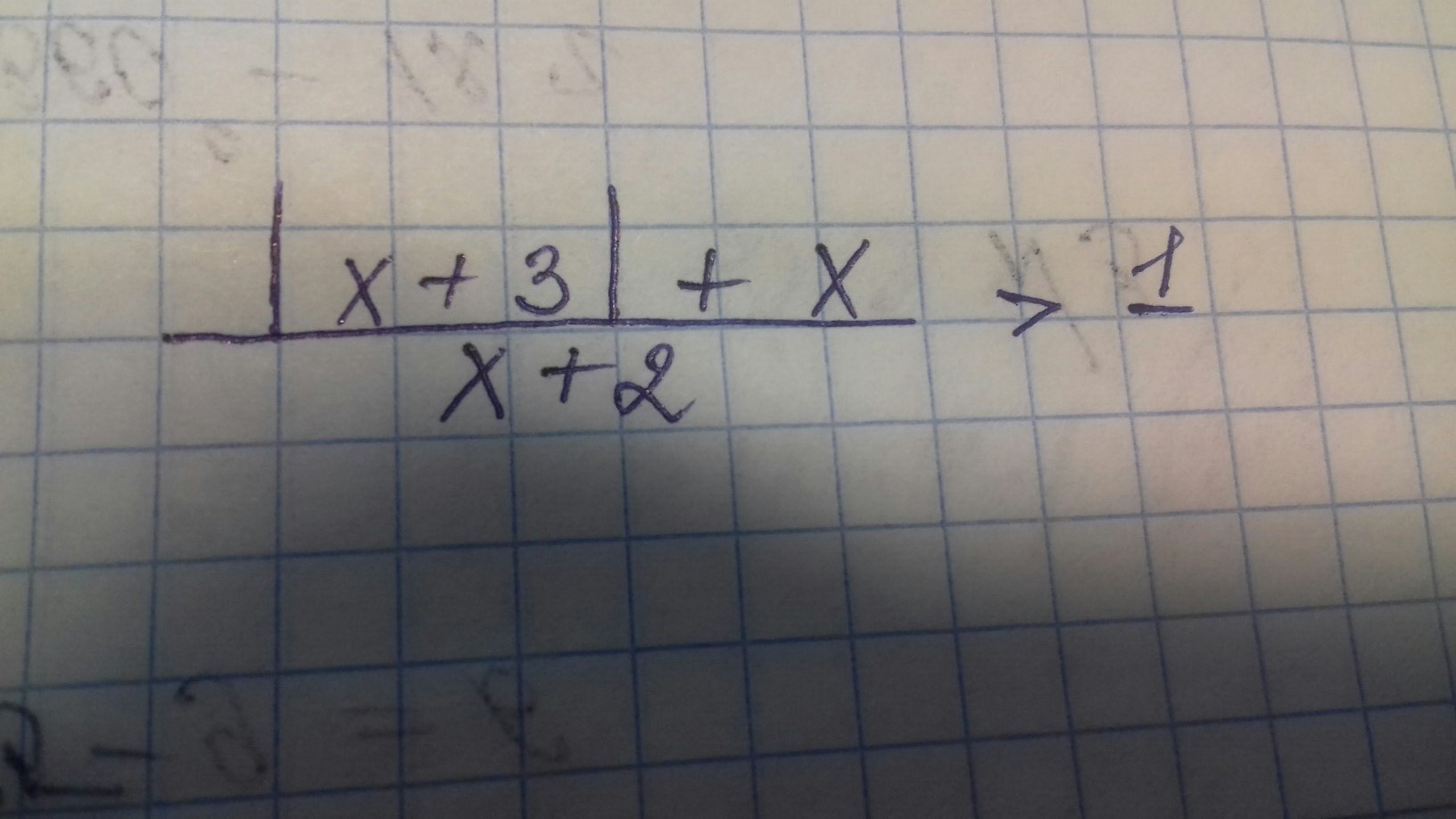
Ответы
Автор ответа:
2
раскроем модуль на промежутках
|x+3|=0; x= -3
___________ -3 ___________
-x-3 x+3
1) x≥ -3
____+____-2___-____-1__+_______
\\\\\\\\\\\\\\\\\ \\\\\\\\\\\\\\\\\
С учетом условия [-3;-2)∪(-1;+oo)
2) x< -3
___-_____ -5 ____+_____-2___-__
С учетом условия (-5;-3)
объединяем два ответа: (-5;-2)∪(-1;+оо)
Автор ответа:
2
⇔
( 1 )
умножая обе части ( 1 ) на положительную при всех х величину
| x+3| +2 , получим : или :
-----------------+++++++++-----------++++++++
-5 -2 -1
Ответ : ( -5 ; -2) ∪ ( -1 ; +∞)
Похожие вопросы
Предмет: Алгебра,
автор: kk7718790
Предмет: Биология,
автор: KlacHbIN
Предмет: Математика,
автор: Retgstufse
Предмет: Литература,
автор: kiselewanastia
Предмет: Математика,
автор: Ранна1