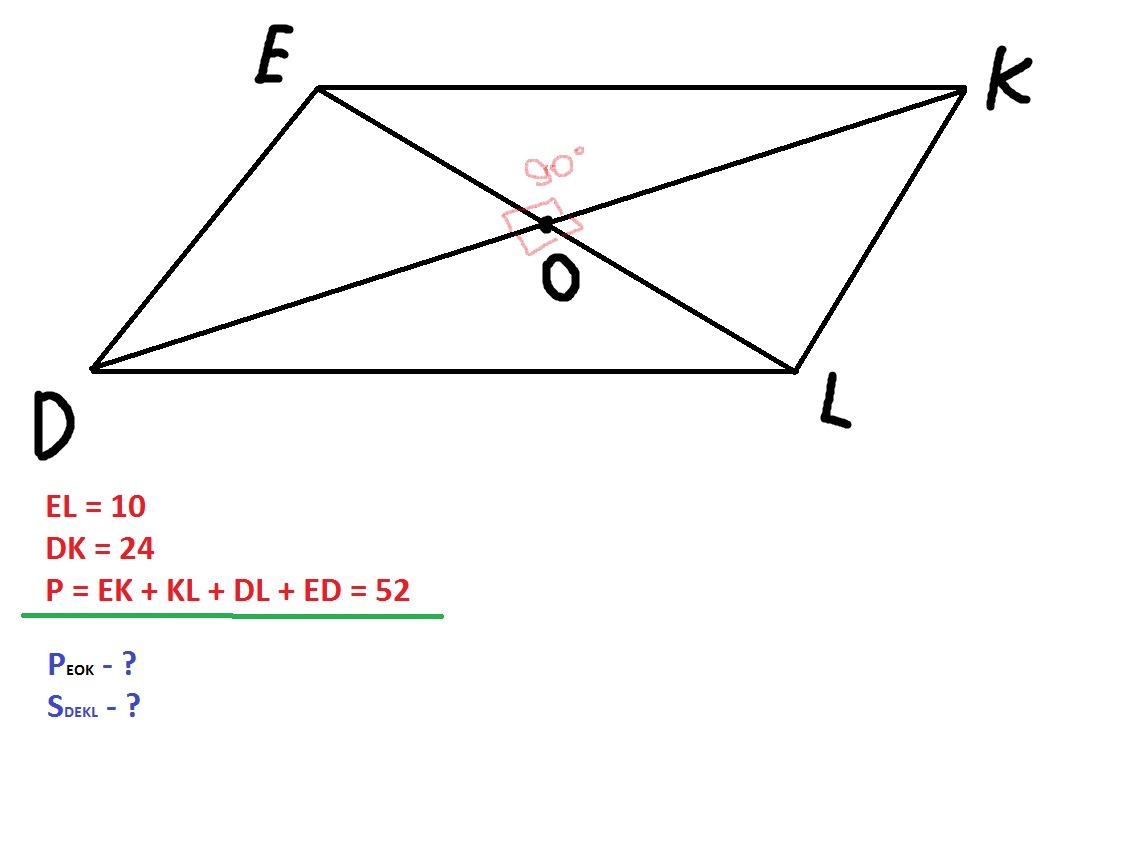
Очень важно....!!!!!!Дан параллелограмм DEKL, O – точка пересечения диагоналей. Диагонали параллелограмма взаимно перпендикулярны и равны 10 см и 24 см. Периметр параллелограмма равен 52 см. Вычисли периметр треугольника EOK и площадь параллелограмма DEKL!
Ответы
Ответ:
Пошаговое объяснение:
Диагонали парал-ма точкой пересечения делятся пополам, тогда ДО=ОК=5, ЕО=ОL=12, из прямоуг. тр-ка ЕОК ЕК^2=EO^2+OK^2=144+25=169, EK=13, Р(ЕОК)=12+5+13=30(см), S(DEKL)=1/2DK*EL=1/2*24*10=120
Ответ:
30 см; 120 см².
Пошаговое объяснение:
Т.к по условию диагонали параллелограмма взаимно перпендикулярны, то углы ∠EOK, ∠KOL, ∠DOL, ∠EOD, = 90°, и следовательно DEKL - ромб (Если у параллелограмма диагонали взаимно перпендикулярны, то он является ромбом).
Рассмотрим треугольник EOK.
Поскольку угол EOK = 90°, то треугольник прямоугольный.
По свойству параллелограмма мы знаем, что диагонали параллелограмма точкой пересечения делятся пополам. Отсюда следует то, что сторона EO = EL : 2 = 10 : 2 = 5 см, а сторона KO = DK : 2 = 24 : 2 = 12 см.
Найдем сторону EK по теореме Пифагора:
EK² = EO² + KO² = 12² + 5² = 144 + 25 = 169.
EK = √169 = 13 см.
Теперь можем найти периметр треугольника : 5 + 12 + 13 = 30 см.
Найдем площадь ромба DEKL:
S = 1/2 * d1 * d2 = 1/2 * 10 * 24 = 120 см.
-------------------------
Другой способ нахождения площади на тот случай, если Вы вдруг забыли свойства ромба.
Найдем площадь параллелограмма:
S = 1/2 * d1 * d2 * sinα = 1/2 * 10 * 24 * sin90° = 1/2 * 10 * 24 * 1 = 120 см².
-------------------------
p.s. - Могли и по другому доказать, что DEKL - ромб, учитывая условие о том, что периметр параллелограмма равен 52.
Это значит, что P = EK + KL + DL + ED = 13 + 13 + DE + KL = 52.
Найдем стороны DE и KL = (52-13-13)/2= 13.
Все стороны равны, а ромбом называется параллелограмм, у которого все стороны равны. Вот так вот.
_______________________________________________
Ответ: Peok = 30 см²; Sdekl = 120 см².