Question

найдите tg угла наклона касательной проведенной в точке x=3, y=x^2-3x-1

Answer 1

Дано: y = x² - 3*x - 1

Xo = 3

Найти: уравнение касательной.

Пошаговое объяснение:

Уравнение касательной

Y = F'(Xo)*(x - Xo) + F(Xo) .

Находим первую производную - k - наклон касательной.

F'(x) = 2*x² - 3.

Вычисляем в точке Хо = 3.

F'(3) = 3 и F(3) = -1.

Записываем уравнения прямой -  касательной.

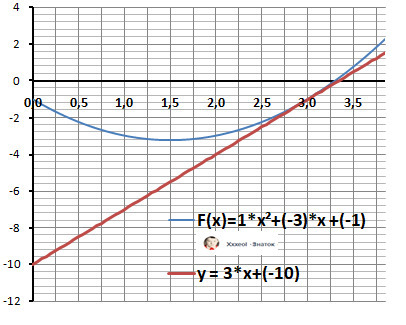
Y = 3*(x - 3) - 1 = 3*x - 10 - касательная

tg α = 3 - тангенс угла - ОТВЕТ

Рисунок к задаче в приложении.