Предмет: Алгебра,
автор: AngelTi
Решите вот такое уравнение
На листке, или подробно распишите, пожалуйста, хочу понять ход решения, для меня он равноценен ответу :)
Ответы
Автор ответа:
1
Сделать замену всей скобки, через замену выразить левую часть, решить уравнение, перейти к обратной замене, решить два уравнения и найти искомые корни.
▪Решение приложено ▪
Приложения:
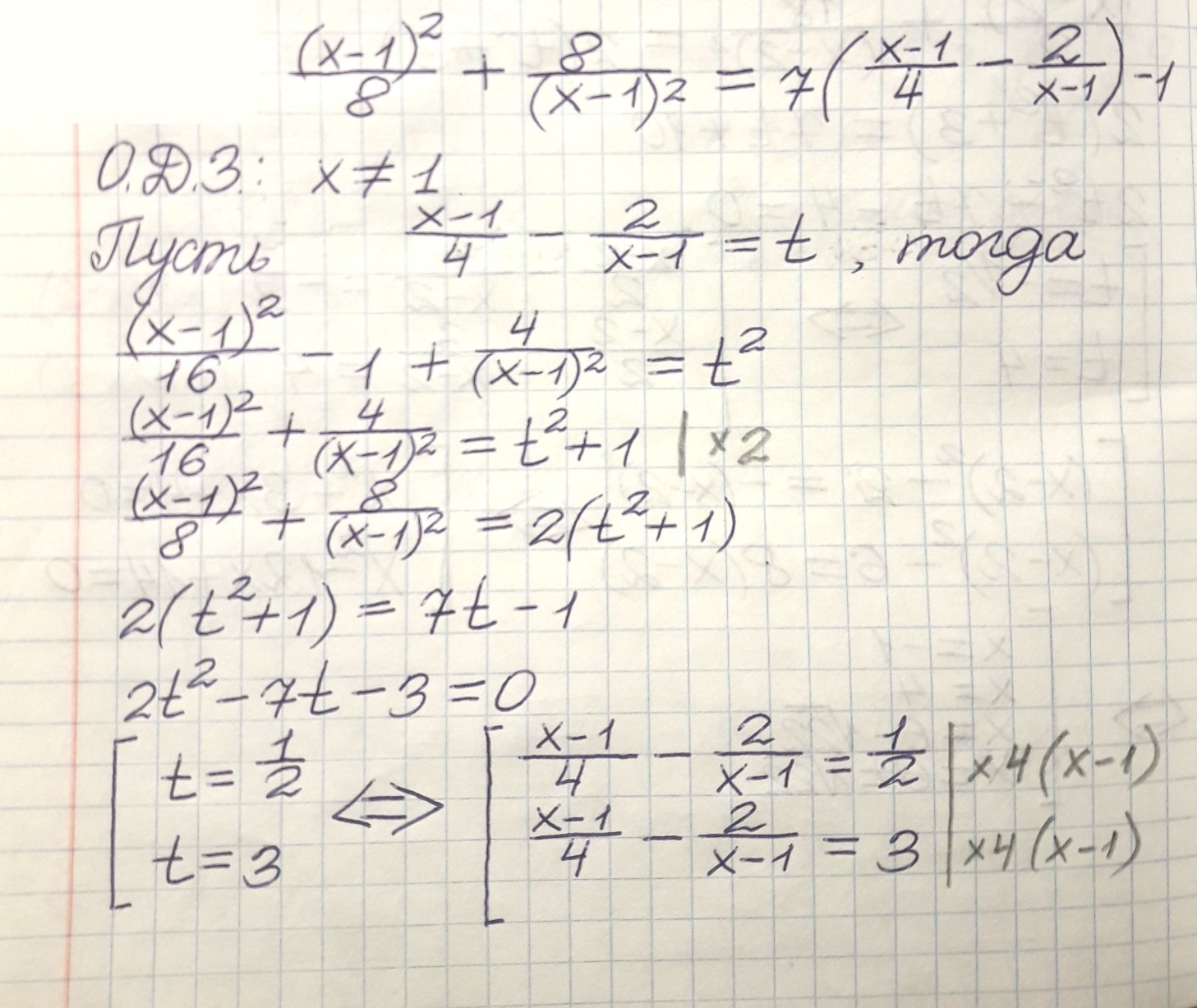
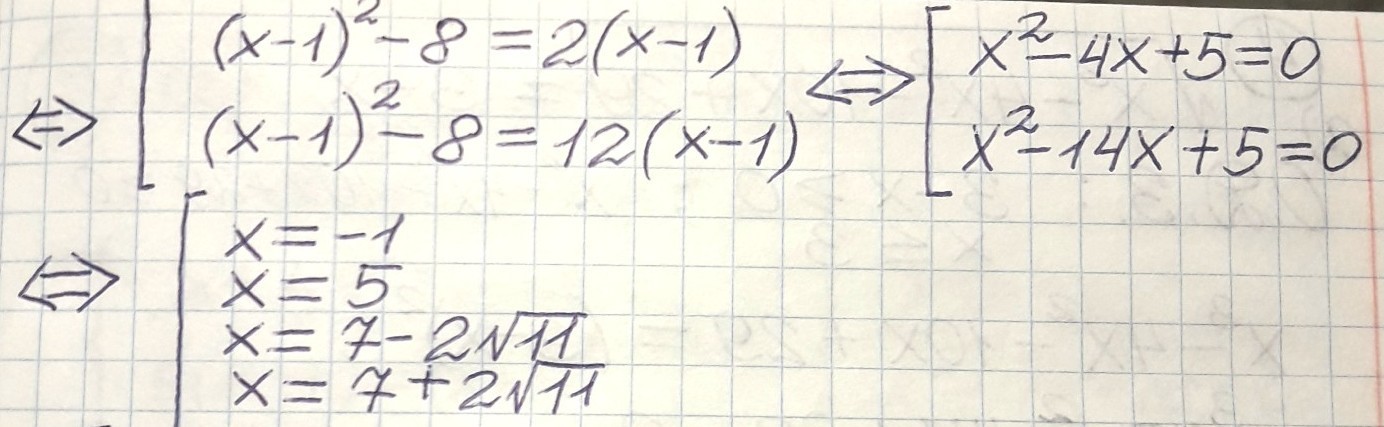
Автор ответа:
1
Замена: , тогда
откуда
Подставляем
Обратная замена
Ответ: 7±2√11; -1; 5
NeZeRAvix:
Какие тут ограничения кроме x≠1?
Интересно, в каком месте это у Вас записано?
Я не написал потому что на корни это не влияет. Был бы посторонний корень - указал бы.
И я не вижу никакой связи с возведением в квадрат. Исходное уравнение ограничено по знаменателю x≠1. Ограничений, возникших по ходу решения, нет.
Вы решаете дробно-рациональное уравнение, не учитывая одз.
Нигде об этом не упомянено.
Я решал с учетом одз, просто не напечатал в решении, потому что она не влияет на ответ. Особо не вижу смысла указывать лишнюю информацию.
За Ваше решение в егэ потеряли бы один балл или даже 2, как Вы знаете.
В егэ нет дробно-рациональных уравнений, если не ошибаюсь. Там тригонометрическое уравнение и логарифмическое неравенство. При решении таких заданий я всегда одз указываю.
В данном же случае не считаю необходимостью
Похожие вопросы
Предмет: Музыка,
автор: selemejana
Предмет: Русский язык,
автор: madinaasirbekova370
Предмет: Геометрия,
автор: auespaevsanhzar100
Предмет: Математика,
автор: мадияр02
Предмет: Алгебра,
автор: dianamelisonsku