Question

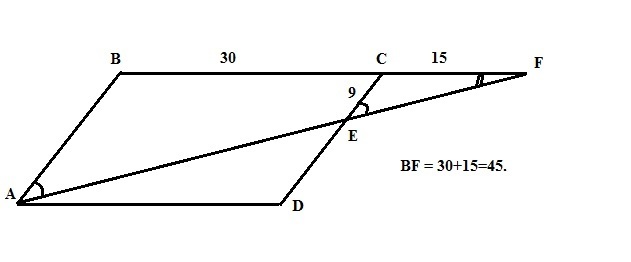
На стороне C D параллелограмма A B C D отмечена точка E . Прямые A E и B C пересекаются в точке F . Найти D E если известно, что E C = 9 , C F = 15 , B C = 30 .

Answer 1

Треугольники АВF и ЕСF подобны, так как СЕ параллельна АВ (прямые, на которых лежат противоположные стороны параллелограмма).

Коэффициент подобия равен  k=BF/CF = 45/15 =3.

Тогда АВ = СЕ*k = 9*3 = 27.  CD= АВ = 27 (как противоположные стороны параллелограмма). Тогда DE = CD - CE = 27-9 =18 ед.

Ответ: DE=18 ед.