Предмет: Математика,
автор: Аноним
Решите срочно!!!! 50 баллов обеспечено
Приложения:
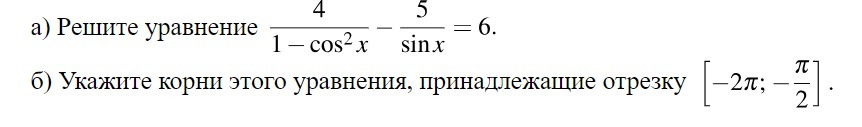
tatsach:
у вас всего 1 балл
Потому как все остальные я потратил я создание ответа
Ответы
Автор ответа:
1
В первом случае решений нет
Выбор корней:
оба корня попадают на интервал [-2π;-π/2]
найдем их
Похожие вопросы
Предмет: Биология,
автор: Аноним
Предмет: Геометрия,
автор: 0510katia1989
Предмет: Математика,
автор: neponasta
Предмет: Математика,
автор: Мариричка