Предмет: Алгебра,
автор: keksiikk
Решите, пожалуйста, тригонометрическое уравнение.
Приложения:
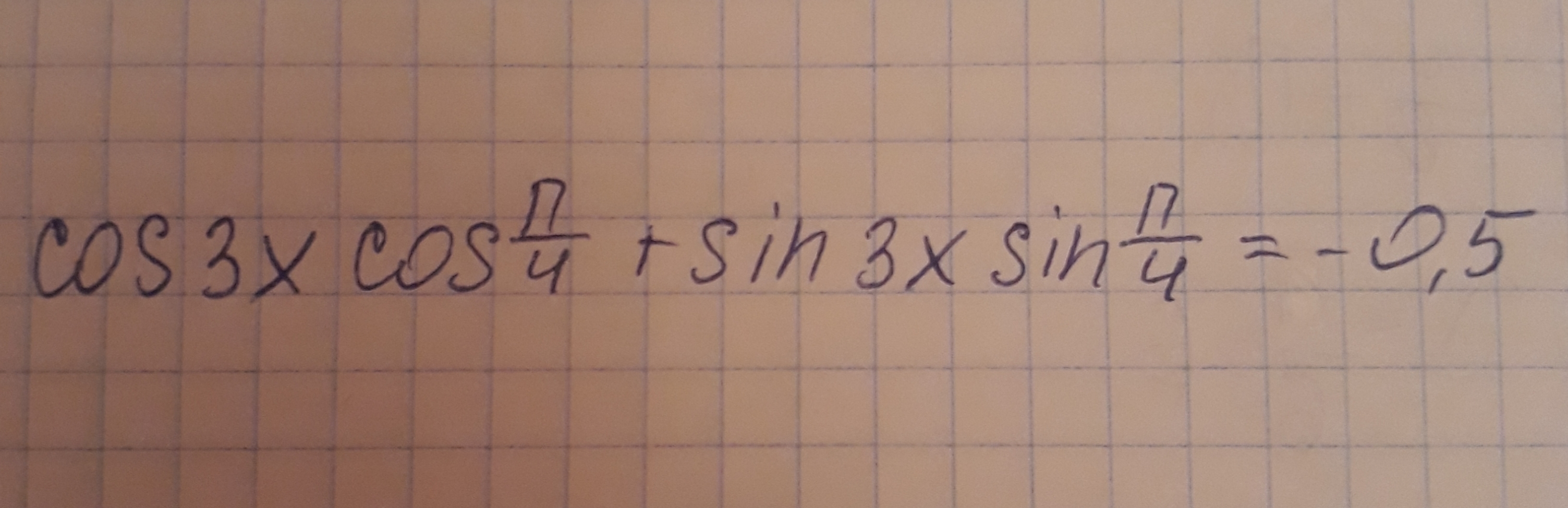
Ответы
Автор ответа:
1
2 строчку получаем из формулы разности аргументов, в данном случае собираем по формуле:
cos(x-y) =cosXcosY+sinXsinY
Приложения:

keksiikk:
Спасибо большое!
Автор ответа:
1
cos(3x)•cos(π/4) + sin(3x)•sin(π/4) = - 0,5
cosα•cosβ + sinα•sinβ = cos(α - β)
cos(3x - (π/4)) = - 1/2
[ 3x - (π/4) = (2π/3) + 2πn ⇔ 3x = (11π/12) + 2πn ⇔ x = (11π/36) + (2πn/3) , n ∈ Z
[ 3x - (π/4) = (-2π/3) + 2πk ⇔ 3x = (-5π/12) + 2πk ⇔ x = (-5π/36) + (2πk/3) , k ∈ Z
ОТВЕТ: (11π/36) + (2πn/3), n ∈ Z ; (-5π/36) + (2πk/3), k ∈ Z
Спасибо большое!
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Биология,
автор: lliza6326
Предмет: Русский язык,
автор: iriskacan
Предмет: Математика,
автор: Аноним