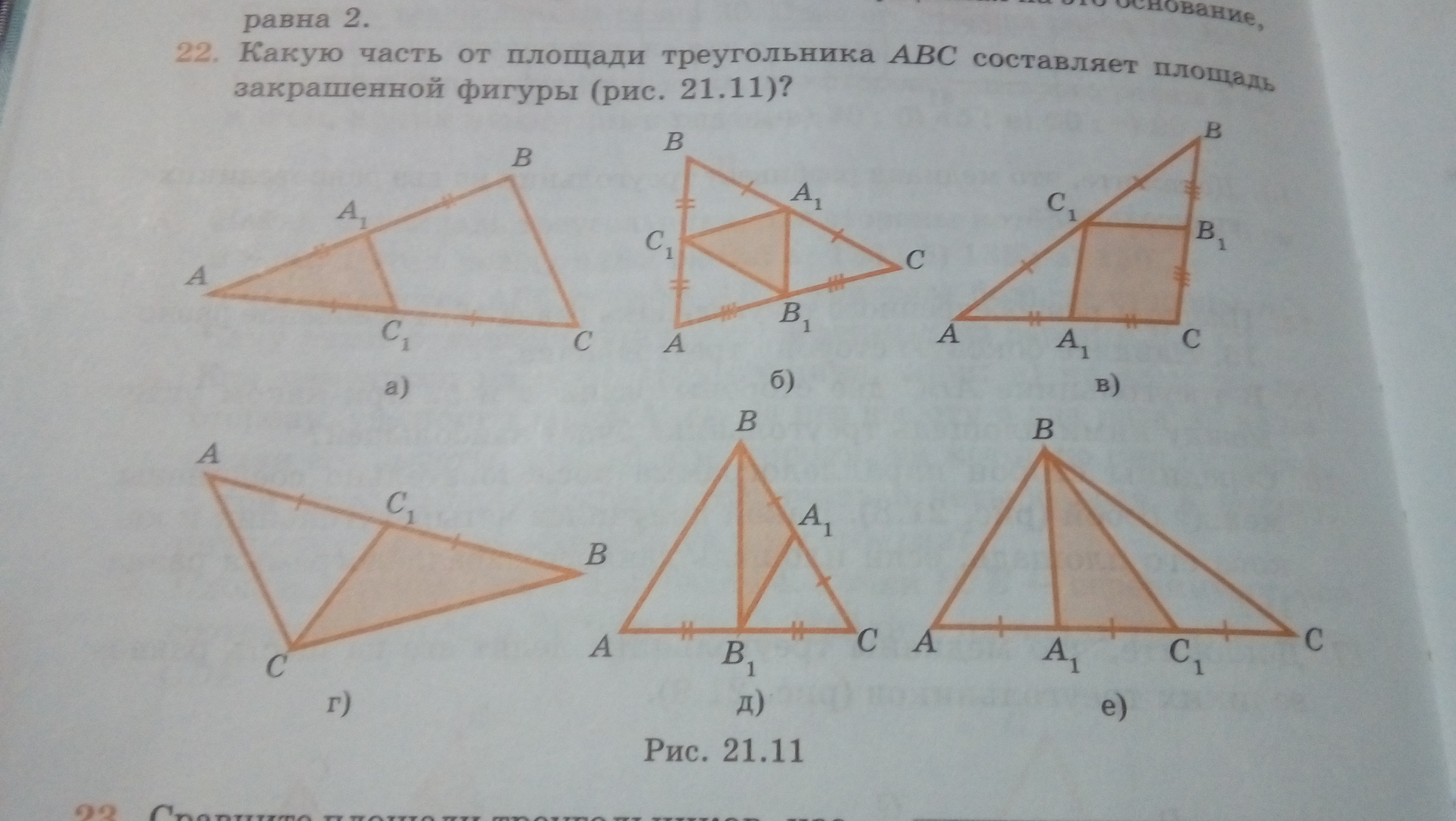
Какую часть от площади треугольника ABC составляет площадь закрашенной фигуры (рис21.11)
Даю 90 баллов! Заранее спасибо!
Ответы
Ответ:
Пошаговое объяснение:
а) 1/4. A1C1 - средняя линия треугольника, ее длина A1C1 = BC/2 - вдвое меньше, чем сторона треугольника.
Высота тр-ка AA1C1 тоже в 2 раза меньше, чем у тр-ка ABC.
Значит, площадь равна S(AA1C1) = 1/2*1/2*S(ABC) = 1/4*S(ABC)
б) 1/4. Все 4 маленьких треугольника одинаковы по площади, каждый равен S(A1B1C1) = 1/4*S(ABC)
в) 1/2. Если мы проведем отрезок CC1, то он разобьет квадрат на два одинаковых треугольника, и каждый будет равен незакрашенному.
S(CC1A1) = S(AC1A1) = S(CC1B1) = S(BC1B1) = 1/4*S(ABC).
S(AC1B1C) = S(CC1A1) + S(CC1B1) = 1/4*S(ABC) + 1/4*S(ABC) = 1/2*S(ABC)
г) 1/2. У треугольника CC1B высота такая же, как у ABC, а основание
BC1 = 1/2*AB. Поэтому площадь
S(CC1B) = 1/2*S(ABC)
д) 1/4. Здесь тоже правило, как в п. г), но его применяем два раза.
S(BB1C) = 1/2*S(ABC); S(A1BB1) = 1/2*S(BB1C) = 1/4*S(ABC)
е) 1/3. И здесь правило такое же, как в п. г), но основание делится на 3.
Поэтому площадь
S(A1BC1) = 1/3*S(ABC)