Question

Пожалуйста помогите срочно. Даю 15 балов. Заранее спасибо.
Подобные треугольники

Установите, истинны или ложны следующие высказывания:


1. Два треугольника называются подобными, если их углы соответственно равны и стороны пропорциональны.

2. Если два треугольника имеют по равному углу, а стороны, заключающие эти углы, пропорциональны, то такие треугольники подобны.

3. Два квадрата всегда подобны.

4. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники подобны.

Answer 1

Ответ:

Всё в разделе "Объяснение".

Объяснение:

1. Неверно.

• Два треугольника называются подобными , если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.

2. Верно.

Это 2 признак подобия треугольников.

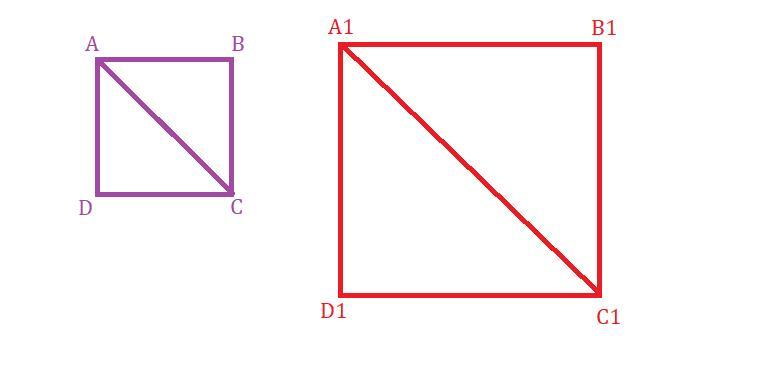
3. Верно.

Даны два квадрата. Назовём их $ABCD$ и $A_1B_1C_1D_1.$

Проведём диагональ $AC$ в квадрате $ABCD$ и диагональ $A_1C_1$ в квадрате $A_1B_1C_1D_1.$

Рассмотрим $\triangle ABC, \triangle ACD, \triangle A_1B_1C_1, \triangle A_1C_1D_1$.

• У квадрата все углы прямые.

$\angle B = \angle B_1 = \angle D = \angle D_1 = 90^{\circ}$, по свойству квадрата.

$\angle ACD = \angle ACB = \angle A_1C_1D_1 = \angle A_1C_1B_1$, так как диагонали квадрата делят углы пополам.

$\Rightarrow \triangle ABC\sim \triangle ACD \sim \triangle A_1B_1C_1 \sim \triangle A_1C_1D_1,$ по 1 признаку подобия треугольников.

$\Rightarrow ABCD\sim A_1B_1C_1D_1.$

4. Неверно.

• Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.