Предмет: Алгебра,
автор: 1CrayZ1
Помогите пожалуйста
Приложения:
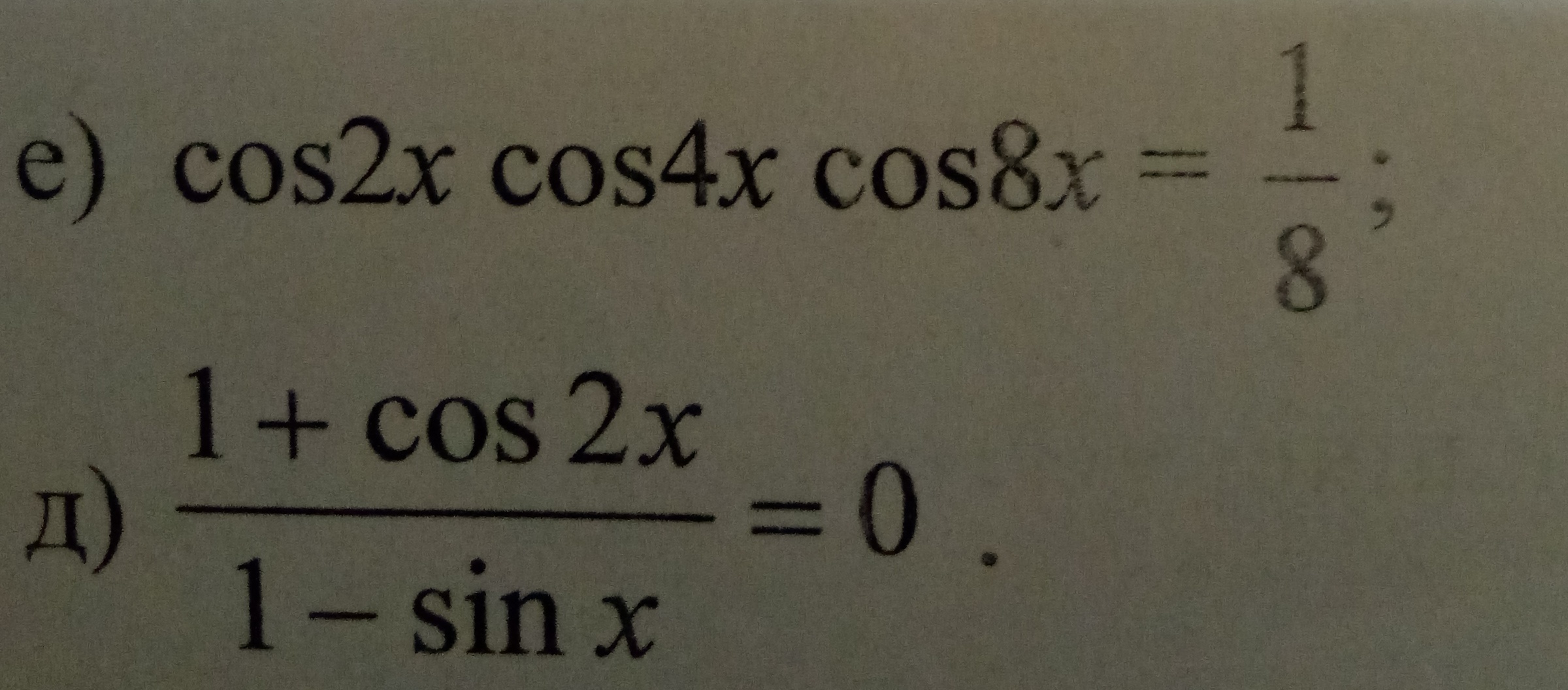
Ответы
Автор ответа:
0
Mihail001192:
Вы не учли ограничение. Допустим k = 4, отсюда x = п/2.
x не= П/2+Пn --> нет решений.
Похожие вопросы
Предмет: Русский язык,
автор: danik2009tomilov
Предмет: Русский язык,
автор: arnurt013
Предмет: Қазақ тiлi,
автор: historiareiss67
Предмет: Математика,
автор: slaavik
Предмет: Математика,
автор: Аноним