Question

Помогите с параметром. 98 баллов
6a+корень из (5+4x-x^2)=ax+3. Найдите все a, при которых уравнение имеет единственный корень.

Answer 1

6a + √(5 + 4x - x²) = ax + 3

√(5 + 4x - x²) = ax - 6a + 3

▪Рассмотрим функцию y = √(5 + 4x - x²)

y² = 5 + 4x - x²

(x² - 4x + 4) + y² = 9

(x - 2)² + y² = 9 - полуокружность при у ≥ 0

Центр полуокружности - О(2;0) с радиусом R = 3

▪Рассмотрим функцию у = ax - 6a + 3

y = a(x - 6) + 3 - множество прямых

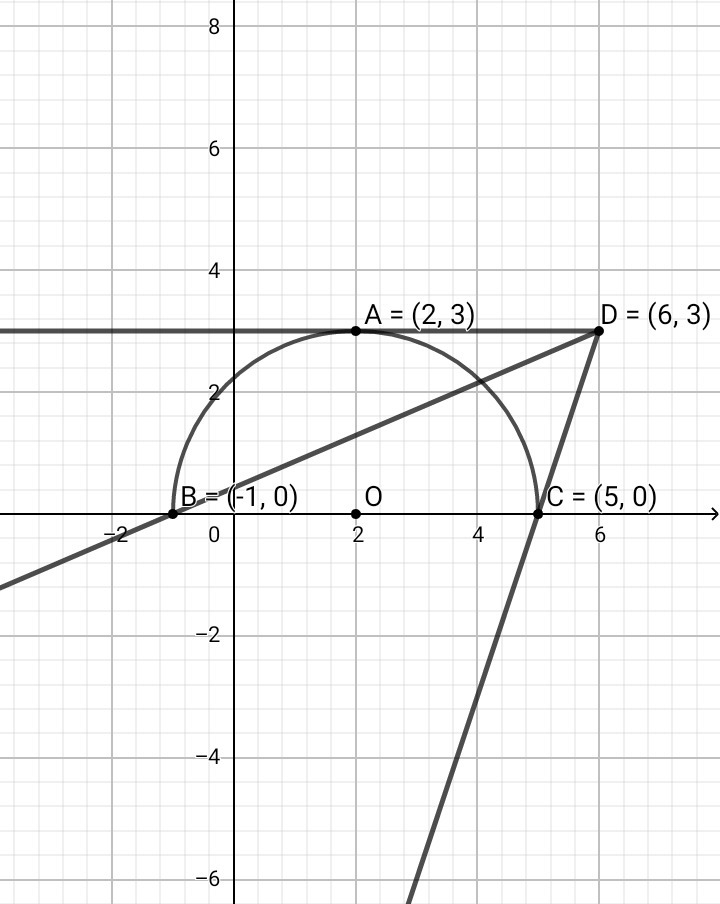
При х = 6 ⇒ у = 3 . Значит, все прямые проходят через точку D(6;3)

Данное уравнение будет иметь единственный корень в том случае, если полуокружность и прямая будут иметь одну общую точку.

▪Полуокружность и прямая DA имеют одну общую точку ⇒ А(2;3), подставляем и находим "а":

3 = а(2 - 6) + 3  ⇒  а = 0

▪Полуокружность и множество прямых, расположенных между прямыми BD и CD, имеют одну общую точку:

B(-1;0) ⇒ 0 = a(-1 - 6) + 3 ;  -7a = - 3  ⇒ a = 3/7

C(5;0) ⇒ 0 = a(5 - 6) + 3 ;  -1a = - 3  ⇒  a = 3

ОТВЕТ: {0} U ( 3/7 ; 3 ]