Question

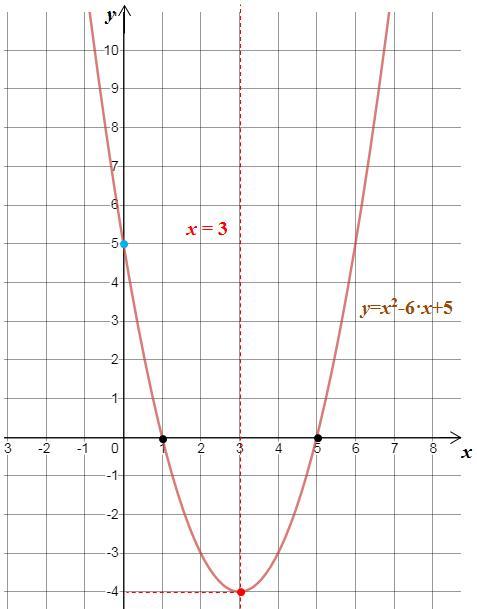
Дана функция у=х( в квадрате) -6х+5
а)Запишите координаты вершины пораболы;
б)определите,в каких четвертях находится график функции.
в)Запишите ось симетрии порабалы;
г)найдите точки пересечения графика с осями координата;
д)постройте график функции(необезательно)

Answer 1

Ответ:

Дана функция у=х²-6·x+5, график которой парабола.

Общий вид параболы: y=a·х²+b·x+c.

а) Находим координаты вершины параболы:

абсцисса вершины параболы $\displaystyle \tt x_0=-\frac{b}{2 \cdot a}= -\frac{-6}{2 \cdot 1}=3;$

ордината вершины параболы y₀=3²-6·3+5=9-18+5=4.

То есть (3; 4) - координаты вершины параболы (на графике красная точка).

б) Найдём точки пересечения графика с осью Ох:

y=0 ⇔ х²-6·x+5=0 ⇔ х²-5·x-x+5=0 ⇔ x·(x-5)-(x-5)=0 ⇔ (x-1)·(x-5)=0 ⇒

⇒ x₁=1 и x₂=5.

Так как вершина параболы расположен в IV четверти и точки пересечения графика с осью Ох положительны (x₁=1 > 0 и x₂=5 > 0), то по свойству параболы график не проходит через III четверть, поэтому график параболы находится в четвертях: I, II и IV (см. рисунок).

в) Ось симметрии параболы прямая x=3 (см. рисунок).

г) Найдём точки пересечения графика с осью Оy:

x=0 ⇔ y(0)=0²-6·0+5=5.

Значит график параболы пересекается с осью Ох в точках (1; 0) и (5; 0) (см. пункт б) и с осью Оy в точке (5; 0) (см. рисунок).

д) Так как коэффициент при x² равен 1>0, то ветви параболы направлены вверх. Для построения графика функции точки определённые в предыдущих пунктах достаточны. Рисунок в приложении.