Question

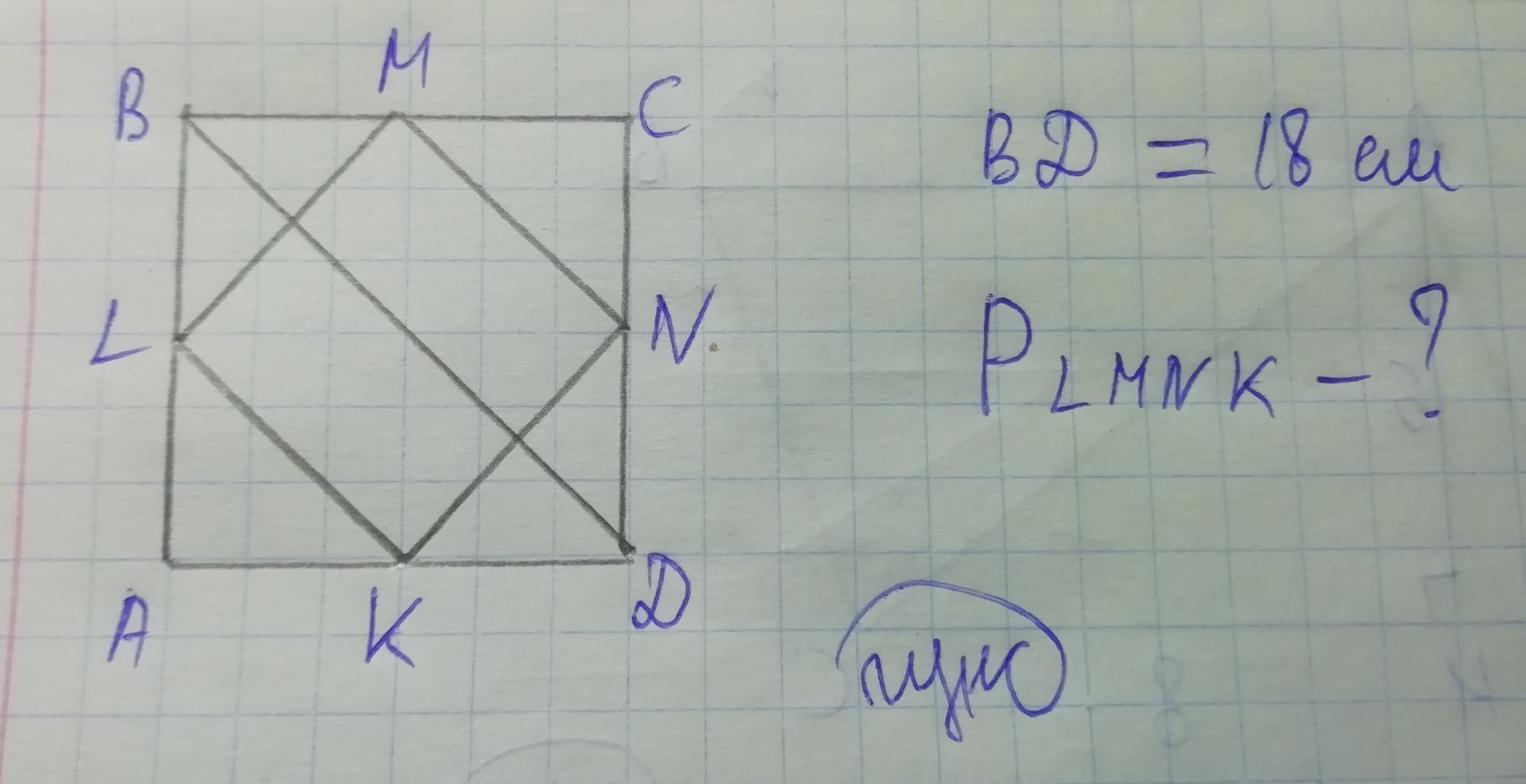
Длина диагонали квадрата равна 18 см.
Вычисли периметр такого квадрата, вершины которого находятся в серединах сторон данного квадрата.

Answer 1

Рассмотрим ΔBCD - прямоугольный: BC = CD (стороны квадрата равны), BD = 18 см

Пусть BC = CD = x. Получим уравнение, взяв один из равных катетов - BD.

BD² = x² + x² (теорема Пифагора)

18² = 2x²

324 = 2x²

$x^{2} =\displaystyle\frac{324}{2} =162\\\\\\x=\sqrt{162}$

BC = CD = √162

BM = MC = CN = ND = DK = AK = AL = LB = √162/2 (по условию)

Рассмотрим ΔLBM - прямоугольный: LB = BM = √162/2, LM - ?

По теореме Пифагора

LM² = LB² + BM²

$LM^{2} =\displaystyle(\frac{\sqrt{162} }{2})^2+(\frac{\sqrt{162} }{2})^2\\\\\\LM^2=\frac{162}{4}+\frac{162}{4} =\frac{324}{4} =81\\\\LM=\sqrt{81} =9$

P(LMNK) = 9 * 4 = 36 см.

Ответ: P = 36 см.