Question

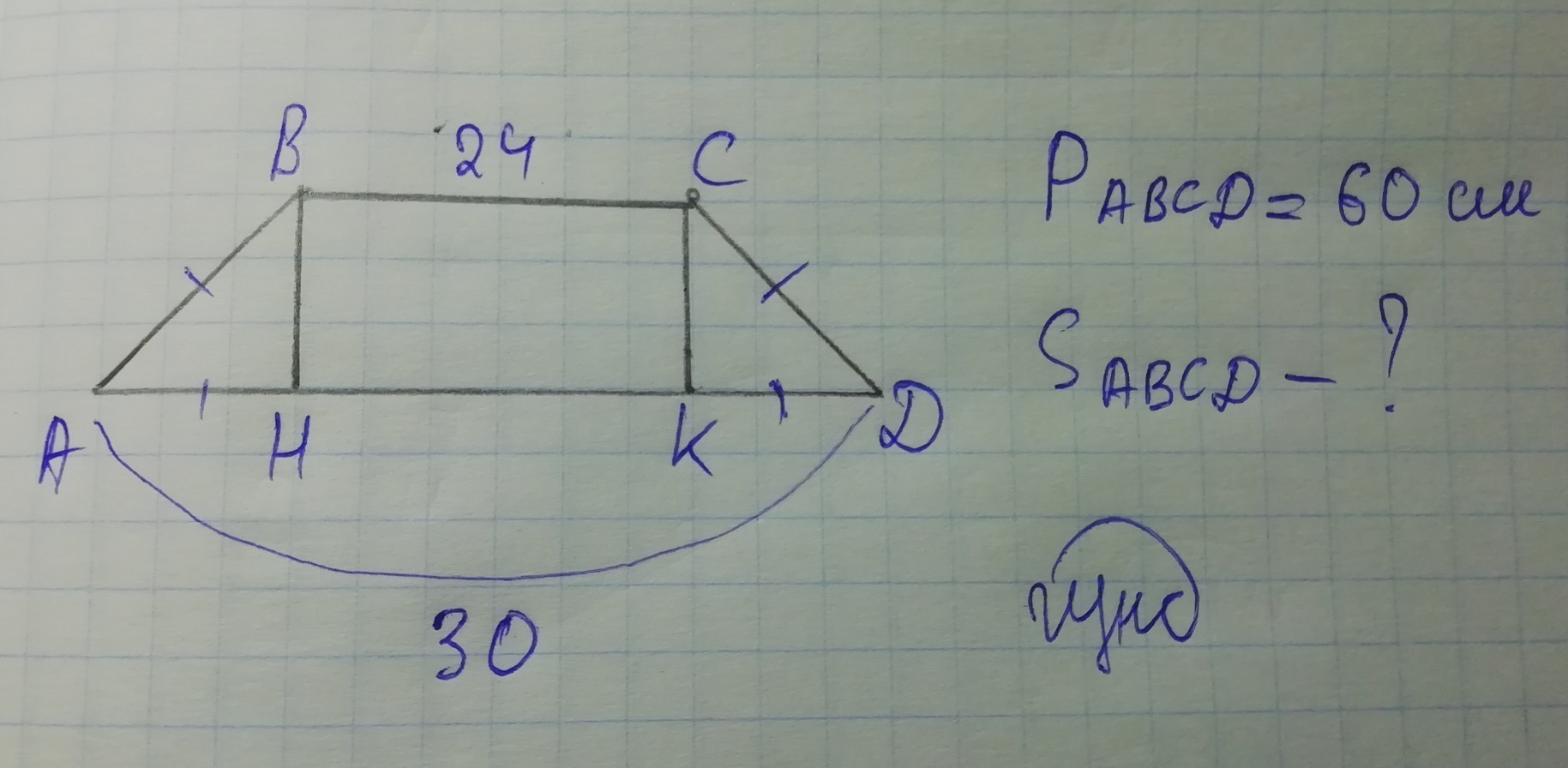
Найдите площадь равнобедренной трапеции, если ее основания равны 24 и 30 см, а периметр 60

Answer 1

Пусть AB = CD = x. Получим уравнение

x + x + 24 + 30 = 60 (в равнобедренной трапеции боковые стороны равны)

2x + 54 = 60

2x = 60 - 54

2x = 6

x = 6/2 = 3

Построим BH и CK - высоты

По свойству равнобедренной трапеции

$AH = KD = \displaystyle \frac{AD-BC}{2} =\frac{30-24}{2} =\frac{6}{2} =3$

Рассмотрим ΔABH - прямоугольный: AB = AH = 3 см, BH - ?

По теореме Пифагора

BH² = AB² + AH²

BH² = 3² + 3²

BH² = 9 + 9 = 18

BH = √18 = 3√2

Формула трапеции:

$S = \displaystyle\frac{1}{2} (BC+AD)\times BH\\\\\\S = \frac{24+30}{2} \times3\sqrt{2} =27\times3\sqrt{2} =81\sqrt{2}$