Предмет: Алгебра,
автор: Аноним
помогите кто чем может срочно
Приложения:
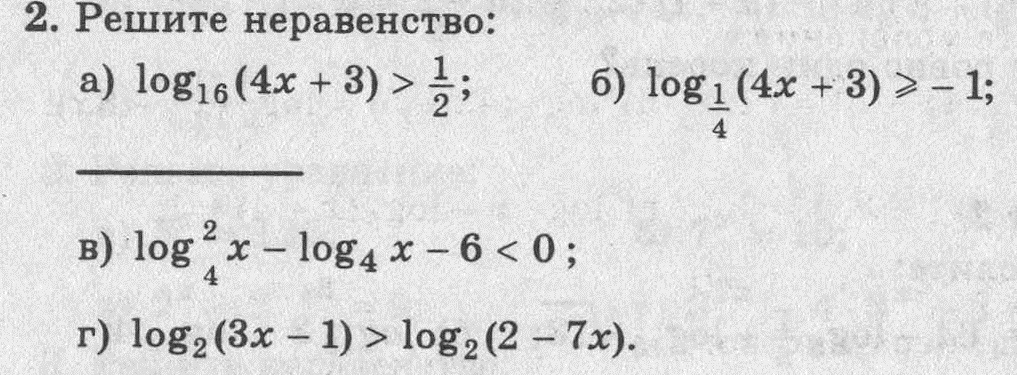
Ответы
Автор ответа:
0
a)
б)
в)
г)
Похожие вопросы
Предмет: Английский язык,
автор: danaanddiana
Предмет: История,
автор: boyka69
Предмет: Математика,
автор: serhiypanchenko09
Предмет: Литература,
автор: юля1953
Предмет: Физика,
автор: chipchilinka228