Предмет: Математика,
автор: romanbratan1
знайти суму цілих розв'язків нерівності (2x+3)^2-(x+2)(x-5)<37
Ответы
Автор ответа:
1
ответ с рисунком на фото
Приложения:
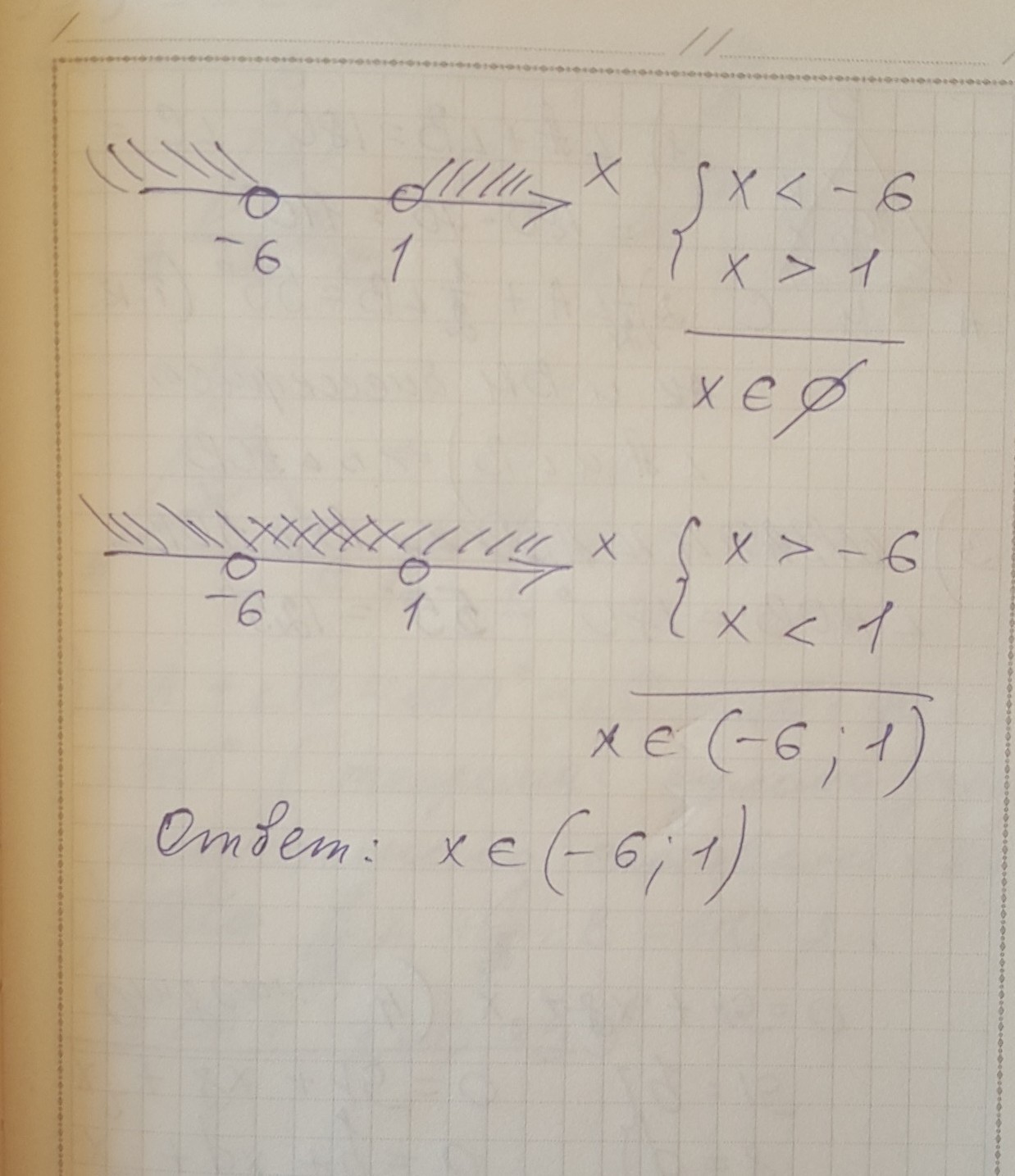
Похожие вопросы
Предмет: Химия,
автор: gojvanovicana0
Предмет: Английский язык,
автор: solloerova
Предмет: История,
автор: sdfdsssss
Предмет: Обществознание,
автор: викторияVikaLove
Предмет: Литература,
автор: elenazubani