помогите, пожалуйста, 395
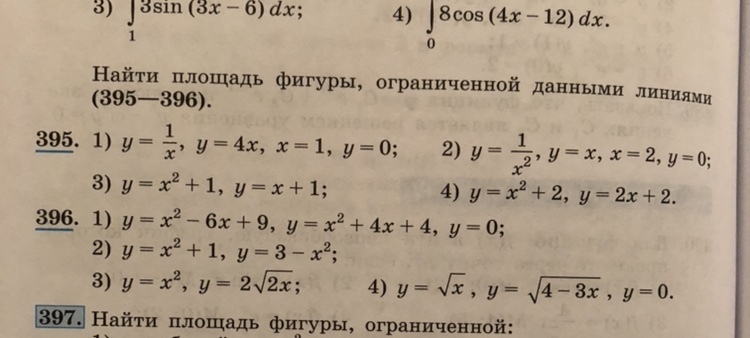
Ответы
При работе с определённым интегралом, всегда лучше делать рисунок. В первом примере, мы имеем гиперболу и "ускоренную" в 4 раза прямую.(то есть функция растёт в 4 раза быстрее по сравнению с y=x).
Если сделать рисунок, то мы увидим, что прямая пересекается с гиперболой. Так как на участке от 0 до 1 гипербола лежит выше прямой, то от точки пересечения до 1, площадь задана гиперболой. То есть, можно вычисление определённого интеграла от 0 до 1, на вычисление двух интегралов. Сначала вычислим точку пересечения с гиперболой.
1/x=4x x =1/2
Получается мы запишем два интеграла для вычисления:
∫4x; ∫1/x; Для первого, область равна от 0 до 1/2; для второго, от 1/2 до 1.
Всё вычислив получим: 1/2 + (㏑1 - ㏑1/2)= 1/2 +㏑2
2) Алгорим тот же.
∫x; ∫1/x^2; Для первого, область от 0 до 1, для второго, от 1 до 2.
Получим 1.
3) Здесь имеем один интеграл для вычисления. Если нарисовать рисунок, то станет видно, что есть две точки пересечения прямой параболой. Точки пересечения и будут нашей областью.
x^2+1=x+1
x=0;1;
∫x+1 - x^2 -1 = 1/2 +1 - 1/3 -1(я вычислил интегралы по отдельности)
В итоге получим:
1/6
4)То же самое что и в примере 3.
x^2+2=2x+2
x=0;2;
∫2x+2 - ∫x^2+2= ∫2x +2 - x^2 - 2 Область будет от 0 до 2.
получим 4+8/3
Объяснял как мог. Если что-то не понятно, то нарисуйте рисунок.