Сумма углов равнобедренной трапеции равна 230° найдите наименьший угол
Ответы
Полное условие :
Сумма двух углов равнобедренной трапеции равна 230°. Найдите наименьший угол. Ответ дайте в градусах.
▔ ▔ ▔
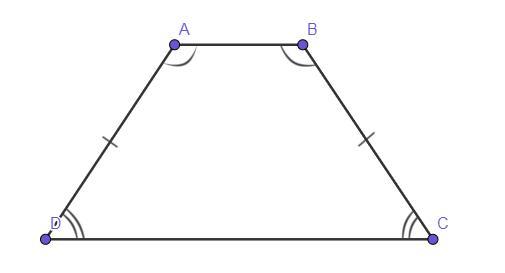
★☆★ Чертёж смотрите во вложении ★☆★
Дано:
Четырёхугольник ABCD — равнобедренная трапеция (AD = BC — боковые стороны, АВ║DC — основания).
Сумма двух углов = 230°.
Найти:
Наименьший угол = ?
Решение:
Рассмотрим пару односторонних углов при основаниях и секущих — боковых сторон.
∠DAB и ∠ADC ; ∠АВС и ∠BCD — каждая из перечисленных пар углов не может давать в сумме 230°, так как по свойству односторонних углов при параллельных прямых они в сумме дают 180°.
Поэтому, пусть —
∠DAB+∠АВС = 230°.
▸В равнобедренной трапеции углы при основании (при любом и каждом) равны◂
На рисунке я выделила их дугами.
Поэтому, имеем, что —
∠DAB = ∠АВС = 230°/2 = 115°
∠ADC = ∠BCD.
▸Сумма углов любого четырёхугольника равна 360°◂
То есть —
∠DAB+∠АВС+∠ADC+∠BCD = 360°
230°+∠ADC+∠BCD = 360°
∠ADC+∠BCD = 360°-230°
∠ADC+∠BCD = 130°
∠ADC = ∠BCD = 130°/2 = 65°.
▸Наименьший угол — угол, который имеет наименьшую градусную меру◂
Таких угла два. ∠ADC = ∠BCD = 65°.
Ответ:
65°.