ПОМОГИТЕ СДЕЛАТЬ ЗАДАНИЕ СОГЛАСНО СХЕМЕ ИССЛЕДОВАНИЯ ФУНКЦИИ
и образец решения во вложении
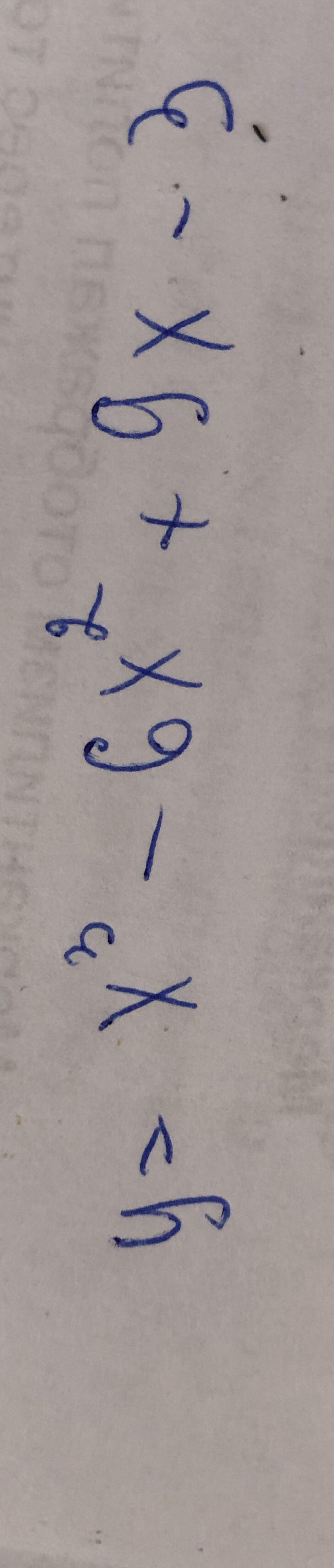


Ответы
ДАНО: Y(x) = 1*x³ -6*x² + 9*x -3 - функция.
ИССЛЕДОВАНИЕ по предложенному в приложении шаблону .
ВНИМАНИЕ!!! Ответ Замятина силой Разума - сначала думаем.
1. Область определения (ООФ) D(y) = R, Х∈(-∞;+∞) - непрерывная , гладкая функция. (Нет деления на 0. R - это все действительные числа, любые, но числа.)
2. Исследование на чётность.
У нечётных функций - все степени при Х - нечётные, у чётных - только не чётные. У нашей функции степени при Х: 3 , 2, 1, 0
Функция общего вида.
Y(-x) ≠ Y(x) - не чётная. Y(-x) ≠ -Y(x), Функция ни чётная, ни нечётная.
3. Исследование на периодичность.
Периодичными являются только тригонометрические функции - sinα, cosα, tgα и другие тригонометрические..
Периода - нет.
4. Точки пересечения с осями координат.
a) Нули функции - пересечение с осью ОХ. Y(x) = 0.
Это самое сложное. Применим тригонометрическую формулу Виета и ... Q=1, R = -0.5, S = 0.75, 'fi' = 0.698 и получаем корни уравнения.
Нули функции: Х₁ ≈ 0,47, Х₂ ≈ 1,65, Х₃ ≈3,88
б) Пересечение с осью ОУ: Y(0) = -3
5. Интервалы знакопостоянства.
Отрицательная - Y(x)<0 X∈(-∞;x₁=0,47] U [x₂=1,65;x₃=3,88]
Положительная -Y(x)>0 X∈[x₁=0,47;x₂=1,65] U [x₃=3,88;+∞)
У чисел ставим квадратные скобки - функция непрерывная.
6. Асимптоты функции.
а) вертикальные - в точках разрыва - нет разрывов - нет.
б) наклонные - по формуле y= k*x + b.
k = lim(+∞)Y(x)/x = x² +.... = ∞ . Наклонных асимптот - нет.
в) горизонтальные - по формуле y = b.
Горизонтальных - нет.
7. Исследование на монотонность по первой производной.
Первая производная. Y'(x) = 3*x² -12*x + 9 = 3*(x²-4x+3) =
= 3*(x-1)*(x-3) = 0 - решаем квадратное уравнение.
Корни производной:Y'(x)=0. Х4=1 Х5=3 - точки экстремумов.
Производная - положительная парабола - ветви вверх, отрицательна между своих корней. Отрицательна - функция убывает, положительна - возрастает.
Интервалы монотонности.
Возрастает Х∈(-∞;x₄=1;]U[x₅=3;+∞) - вне корней производной,
убывает - Х∈[x₄=1;x₅=3] - между корнями производной.
8. Локальные экстремумы.
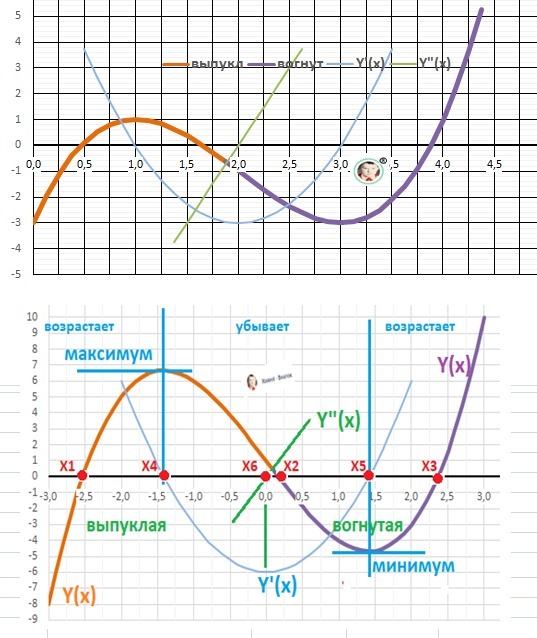
Максимум Ymax(X₄=1) = 1. Минимум Ymin(X₅=3) =-3
9. Точки перегиба по второй производной функции.
Y"(x) = 6* x -12 = 6*(х - 2) = 0
Корень производной - точка перегиба Х₆=2
Вогнутая при положительной производной. Вспоминаем функцию y = x² - у неё y"(x) = 2 - парабола вогнутая - "ложка".
Выпуклая “горка» Х∈(-∞; Х₆=2]
Вогнутая – «ложка» Х∈[Х₆=2; +∞).
11. График в приложении.