Предмет: Математика,
автор: Barby1978
1)Найдите то значение , главное значение аргумента которого минимально. В ответе укажите его мнимую часть. (1файл)
2)Вычислите указанную степень числа i. j^136=?
3)Найдите остаток от деления многочлена P(x) = 5x^71 – 2x^30 + 7x^5 + 20 на линейный многочлен (x + 1)
4)Найдите главное значение аргумента комплексного числа z = – 1 + i. В ответ введите множитель при числе π.
Приложения:
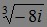
Ответы
Автор ответа:
0
Ответ:
3. Остаток будет равен значению многочлена при а=-1, т.е.
P(-1)=5*(-1)⁷¹ -2(-1)³⁰+7(-1)⁵+20=-5-2-7+20=6
Пошаговое объяснение:
Barby1978:
вы знаете только задание 3?
Похожие вопросы
Предмет: Биология,
автор: morozovamarija2010
Предмет: Русский язык,
автор: CoMeR050
Предмет: Математика,
автор: arinagrishhenko
Предмет: Математика,
автор: Жасмина11th
Предмет: Математика,
автор: азиза1232